题目内容
16.解方程(1)4x-3(19-x)=6x-7(9-x)
(2)$\frac{2}{3}[{\frac{3}{2}({x-4})-6}]=2x+1$
(3)$\frac{x}{2}=\frac{x+3}{4}-\frac{2-3x}{6}$
(4)$\frac{2x+1}{4}-1=x-\frac{10x+1}{12}$.
分析 (1)首先去括号,然后再移项,注意移项要变号,然后合并同类项、系数化为1即可;
(2)首先去括号,然后再移项,注意移项要变号,然后合并同类项、系数化为1即可;
(3)首先乘以12去分母,再去括号,然后再移项,注意移项要变号,然后合并同类项、系数化为1即可;
(4)首先乘以12去分母,再去括号,然后再移项,注意移项要变号,然后合并同类项、系数化为1即可.
解答 解:(1)去括号得:4x-57+3x=6x-63+7x,
移项得:4x+3x-7x-6x=-63+57,
合并同类项得:-6x=-6,
把x的系数化为1得:x=1;
(2)去括号得:x-4-4=2x+1,
移项得:x-2x=1+4+4,
合并同类项得:-x=9,
把x的系数化为1得x=-9;
(3)去分母得:6x=3(x+3)-2(2-3x),
去括号得:6x=3x+9-4+6x,
移项得:6x-3x-6x=9-4,
合并同类项得:-3x=5,
把x的系数化为1得x=-$\frac{5}{3}$;
(4)去分母得:3(2x+1)-12=12x-(10x+1),
去括号得:6x+3-12=12x-10x-1,
移项得:6x-12x+10x=-1+12-3,
合并同类项得:4x=8,
把x的系数化为1得x=2.
点评 此题主要考查了解一元一次方程,解一元一次方程的一般步骤:去分母、去括号、移项、合并同类项、系数化为1.

练习册系列答案
相关题目
1.在多项式x3-xy2+25中,常数项是( )
| A. | 25 | B. | x3,xy2 | C. | x3,-xy2 | D. | x3 |
 作图:将△ABC平移,使点B到达点E的位置,画出平移后的图形.
作图:将△ABC平移,使点B到达点E的位置,画出平移后的图形.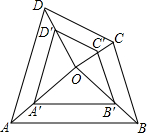 如图,点O是四边形ABCD与A′B′C′D′的位似中心,3OA′=2OA,则$\frac{A'B'}{AB}$=$\frac{2}{3}$.
如图,点O是四边形ABCD与A′B′C′D′的位似中心,3OA′=2OA,则$\frac{A'B'}{AB}$=$\frac{2}{3}$.