题目内容
在平面直角坐标系中，若点P（m-2，m+1）在第二象限，则m的取值范围是（ ）
| A、m＜2 | B、-2＜m＜1 |
| C、-1＜m＜2 | D、m＞-1 |
考点：点的坐标,解一元一次不等式组
专题：
分析：根据第二象限内点的横坐标是负数，纵坐标是正数列出不等式组求解即可．
解答：解：∵点P（m-2，m+1）在第二象限，
∴
，
解得-1＜m＜2．
故选C．
∴
|
解得-1＜m＜2．
故选C．
点评：本题考查了各象限内点的坐标的符号特征以及解不等式，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（-，+）；第三象限（-，-）；第四象限（+，-）．
练习册系列答案
相关题目
如图，△DAC和△EBC均是等边三角形，AE、BD分别与CD、CE交于点M、N，且A、C、B在同一直线上，有如下结论：①△ACE≌△DCB； ②CM=CN；③AC=DN； ④PC平分∠APB； ⑤∠APD=60°．其中不正确结论是
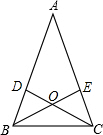如图，在△ABC中，AB=AC，∠A=36°，两条角平分线BE、CD相交于点O，则图中全等等腰三角形有（ ）| A、1对 | B、2对 | C、3对 | D、4对 |
实数1-
位于（ ）
| 12 |
| A、-5与-4之间 |
| B、-4与-3之间 |
| C、-3与-2之间 |
| D、-2与-1之间 |
下列哪种几何体的截面不可能是长方形（ ）
| A、长方体 | B、正方体 |
| C、圆柱 | D、圆锥 |
下列各式能运用平方差公式分解因式的有（ ）
①x2-2xy+y2 ②-4x2+y2 ③-4x2-y2 ④（x-y）3-y+x．
①x2-2xy+y2 ②-4x2+y2 ③-4x2-y2 ④（x-y）3-y+x．
| A、1个 | B、2个 | C、3个 | D、4个 |