题目内容
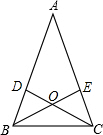 如图,在△ABC中,AB=AC,∠A=36°,两条角平分线BE、CD相交于点O,则图中全等等腰三角形有( )
如图,在△ABC中,AB=AC,∠A=36°,两条角平分线BE、CD相交于点O,则图中全等等腰三角形有( )| A、1对 | B、2对 | C、3对 | D、4对 |
考点:等腰三角形的判定与性质
专题:
分析:由在△ABC中,AB=AC,∠A=36°,角平分线BD与CE相交于点O,利用等边对等角与角平分线的性质,易求得图中各角的度数,然后利用等角对等边的知识,即可判定△ABC,△ABE,△ACD,△BCD,△BCE,△OBC,△OBD,△OCE都是等腰三角形.
解答:解:∵在△ABC中,AB=AC,∠A=36°,
∴∠ABC=∠ACB=
(180°-∠A)=72°,
∵△ABC的角平分线BE与CD相交于点O,
∴∠ABE=∠EBC=
∠ABC=36°,∠ACD=∠BCD=
∠ACB=36°,
∴∠BDC=∠BEC=180°-36°-72°=72°,
∴∠A=∠ABE=∠EBC=∠BCD=∠ACD=36°,∠ABC=∠ACB=∠BEC=∠BDC=72°,
∴∠DOB=∠EOC=180°-72°-36°=72°,
∴AE=BE,AD=CD,BD=OB=OC=CE,CD=BC=BE,
∴等腰三角形有:△ABC,△ABE,△ACD,△BCD,△BCE,△OBC,△OBD,△OCE共8个,其中△ABE≌△ACD,
△BCD≌△BCE,△OBD≌△OCE;
故选:C.
∴∠ABC=∠ACB=
| 1 |
| 2 |
∵△ABC的角平分线BE与CD相交于点O,
∴∠ABE=∠EBC=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠BDC=∠BEC=180°-36°-72°=72°,
∴∠A=∠ABE=∠EBC=∠BCD=∠ACD=36°,∠ABC=∠ACB=∠BEC=∠BDC=72°,
∴∠DOB=∠EOC=180°-72°-36°=72°,
∴AE=BE,AD=CD,BD=OB=OC=CE,CD=BC=BE,
∴等腰三角形有:△ABC,△ABE,△ACD,△BCD,△BCE,△OBC,△OBD,△OCE共8个,其中△ABE≌△ACD,
△BCD≌△BCE,△OBD≌△OCE;
故选:C.
点评:此题考查了等腰三角形的性质与判定以及角平分线的定义.此题难度适中,注意数形结合思想的应用,小心别漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平面直角坐标系中,若点P(m-2,m+1)在第二象限,则m的取值范围是( )
| A、m<2 | B、-2<m<1 |
| C、-1<m<2 | D、m>-1 |
若(2a-3b)2+A=4a2+ab+9b2,则A为( )
| A、5ab | B、11ab |
| C、-11ab | D、13ab |
抛物线y=-2(x+1)2+3的顶点坐标是( )
| A、(1,3) |
| B、(-1,-3) |
| C、(-2,3) |
| D、(-1,3) |
下列图形中不可能拼成正方体的是( )
A、 |
B、 |
C、 |
D、 |
若a2+6ab+m2=(a+3b)2,则m的值为( )
| A、2b |
| B、3b |
| C、9b2 |
| D、3b2 |