题目内容
2.在平行四边形ABCD中,BC边上的高AE=3,AD=5,∠ABE为45°,若以点E为原点,BC所在直线为x轴,AE所在直线为y轴,请:(1)建立平面直角坐标系,并画出图形;
(2)分别求出平行四边形ABCD四个顶点的坐标.
分析 (1)首先以点E为原点,BC所在直线为x轴,AE所在直线为y轴建立平面直角坐标系,再根据已知条件中的数据画图即可;
(2)过点D作DF⊥EC于点F,由已知条件易证△AEB为等腰直角三角形,所以BE的长可知,再分别求出CE,DF的长即可得到平行四边形ABCD四个顶点的坐标.
解答 解:(1)如图所示: (2)∵AE=3,
(2)∵AE=3,
∴点A的坐标为(0,3),
∵AE⊥BE,∠ABE=45°,
∴△AEB为等腰直角三角形,
∴AE=BE=3,
∴点B的坐标为(-3,0),
∵四边形ABCD是平行四边形,
∴AD=BC=5,
∴CE=2,
∴点C的坐标为(2,0),
过点D作DF⊥EC于点F,则DE=AE=3,AD=EF=5,
∴点D的坐标为(5,3).
点评 本题考查了平行四边形的性质、等腰直角三角形的判断和性质以及考查坐标与图形的性质等知识点,正确作出图形的辅助线是解题的关键.

练习册系列答案
相关题目
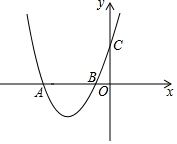 如图,抛物线M:y=(x+1)(x+a)(a>1)交x轴于A、B两点(A在B的左边),交y轴于C点.抛物线M关于y轴对称的抛物线N交x轴于P、Q两点(P在Q的左边)
如图,抛物线M:y=(x+1)(x+a)(a>1)交x轴于A、B两点(A在B的左边),交y轴于C点.抛物线M关于y轴对称的抛物线N交x轴于P、Q两点(P在Q的左边)