题目内容
如图,在⊙O中,
 =
=
 ,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.
,∠ACB=60°,求证:∠AOB=∠BOC=∠AOC.


【考点】圆心角、弧、弦的关系.
【专题】证明题.
【分析】根据弧相等,则对应的弦相等从而证明AB=AC,则△ABC易证是等边三角形,然后根据同圆中弦相等,则对应的圆心角相等即可证得.
【解答】证明:∵
 =
=
 ,
,
∴AB=AC
∴△ABC是等腰三角形
∵∠ACB=60°
∴△ABC是等边三角形,
∴AB=BC=CA
∴∠AOB=∠BOC=∠COA.
【点评】本题考查了圆心角、弧、弦的关系以及等边三角形的判定,正确理解圆心角、弧、弦的关系是关键.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
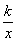 (k为常数,且
(k为常数,且 k≠0)的图象位于第一、三象限,请写出一个符合
k≠0)的图象位于第一、三象限,请写出一个符合