��Ŀ����
ij�̳���װ������һ�����Ƴ�����ƽ��ÿ����۳�20����ÿ��ӯ��40Ԫ��Ϊ���������ۣ��̳������������ۣ������飬ÿ����������1Ԫʱ��ƽ��ÿ��ɶ�����2����
��1����ÿ����������xԪ���̳���װ��ÿ��ӯ��yԪ�������y��x֮��ĺ�����ϵʽ��
��2�����̳�ÿ��Ҫӯ��1200Ԫ��ÿ������Ӧ���۶���Ԫ��
��3����ÿ���������۶���Ԫʱ���̳�ÿ���ӯ���ﵽ������ӯ���Ƕ���Ԫ��
��
�����㡿���κ�����Ӧ�ã�
��ר�⡿�������⣮
����������1����ÿ����xԪ����ʾ�����ۺ��ӯ�������۵�������Ȼ�����ÿ���ӯ������ÿ��ӯ�������������ó�y��x�ĺ�����ϵ���ɣ�
��2����y=1200�����ݣ�1���ĺ�����ϵ����Ա�����ȡֵ���ɣ�
��3�������䷽��������κ�������ֵ�������ó��𰸣�
����𡿽⣺��1����ÿ����xԪ���̳�ƽ��ÿ��Ӯ��yԪ��
��y=��40��x����20+2x��=��2x 2+60x+800��
��2����y=1200��
1200=��2��x��15��2+1250��
���x1=10��x2=20��
��ΪΪ���������ۣ����ԣ�Ӧ����20Ԫ��
���̳�ÿ��ƽ����ӯ��1200Ԫ��ÿ������Ӧ����20Ԫ��
��3��y=��2x 2+60x+800��
=��2��x��15��2+1250��
��x=15ʱ��y�����ֵΪ1250Ԫ��
��ÿ������15Ԫʱ���̳�ƽ��ÿ��ӯ����࣮
�����������⿼���˶��κ�����Ӧ���Լ����κ�������ֵ���⣬��ʾ�����ۺ��ӯ�������۵�������Ȼ��õ�ƽ��ÿ���ӯ���뽵��֮��ĺ�����ϵʽ�ǽ���Ĺؼ���

 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д� ��
�� ����
���� ��0.
��0. ���������ĸ�����( )
���������ĸ�����( )
 =
=



 ��y2=
��y2=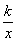 �ڵ�һ����ͼ������y1=
�ڵ�һ����ͼ������y1=