题目内容
 如图,抛物线与直线都经过坐标轴的正半轴上A(4,0),B两点,该抛物线的对称轴x=-1,与x轴交于点C,且∠ABC=90°,求:
如图,抛物线与直线都经过坐标轴的正半轴上A(4,0),B两点,该抛物线的对称轴x=-1,与x轴交于点C,且∠ABC=90°,求:(1)直线AB的解析式;
(2)抛物线的解析式.
考点:待定系数法求二次函数解析式,待定系数法求一次函数解析式
专题:计算题
分析:(1)先证明Rt△CBO∽Rt△BAO,利用相似比计算出OB=2,则B点坐标为(2,0),然后利用待定系数法确定直线AB的解析式;
(2)先利用对称性得到抛物线与x轴的另一个交点坐标为(-6,0),则可设交点式y=a(x+6)(x-4),然后把B点坐标代入求出a即可.
(2)先利用对称性得到抛物线与x轴的另一个交点坐标为(-6,0),则可设交点式y=a(x+6)(x-4),然后把B点坐标代入求出a即可.
解答:解:(1)∵A点坐标为(4,0),C点坐标为(-1,0),
∴OA=4,OC=1,
∵∠ABC=90°,
∴∠CBO=∠BAO,
∴Rt△CBO∽Rt△BAO,
∴OB:OA=OC:OB,即OB:4=1:OB,
∴OB=2,
∴B点坐标为(2,0),
设直线AB的解析式为y=mx+n,
把A(4,0)、B(0,2)代入得
,解得
,
∴直线AB的解析式为y=-
x+2;
(2)∵该抛物线的对称轴x=-1,
而A点坐标为(4,0),
∴抛物线与x轴的另一个交点坐标为(-6,0),
设抛物线的解析式为y=a(x+6)(x-4),
把B(0,2)代入得a•6•(-4)=2,解得a=-
,
所以抛物线的解析式为y=-
(x+6)(x-4)=-
x2-
x+2.
∴OA=4,OC=1,
∵∠ABC=90°,
∴∠CBO=∠BAO,
∴Rt△CBO∽Rt△BAO,
∴OB:OA=OC:OB,即OB:4=1:OB,
∴OB=2,
∴B点坐标为(2,0),
设直线AB的解析式为y=mx+n,
把A(4,0)、B(0,2)代入得
|
|
∴直线AB的解析式为y=-
| 1 |
| 2 |
(2)∵该抛物线的对称轴x=-1,
而A点坐标为(4,0),
∴抛物线与x轴的另一个交点坐标为(-6,0),
设抛物线的解析式为y=a(x+6)(x-4),
把B(0,2)代入得a•6•(-4)=2,解得a=-
| 1 |
| 12 |
所以抛物线的解析式为y=-
| 1 |
| 12 |
| 1 |
| 12 |
| 1 |
| 6 |
点评:本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
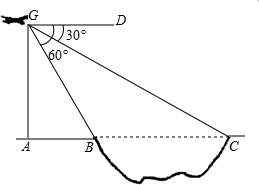 如图,为测得某一湖泊的宽度,在A处的正上方G处有一架飞行的飞机,此时正好测得湖泊东岸的点C处的俯角为30°,湖泊西岸的点B处的俯角为60°,此时飞机离地面的高度为900米,则湖泊的宽度是多少米?
如图,为测得某一湖泊的宽度,在A处的正上方G处有一架飞行的飞机,此时正好测得湖泊东岸的点C处的俯角为30°,湖泊西岸的点B处的俯角为60°,此时飞机离地面的高度为900米,则湖泊的宽度是多少米?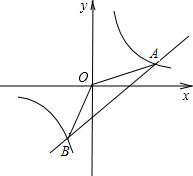 如图,已知A(4,a),B(-2,-4)是一次函数y1=kx+b的图象和反比例函数y2=
如图,已知A(4,a),B(-2,-4)是一次函数y1=kx+b的图象和反比例函数y2= 如图,两建筑物的水平距离BC为18m,从A点测得D点的俯角α为30°,测得C
如图,两建筑物的水平距离BC为18m,从A点测得D点的俯角α为30°,测得C