题目内容
设有n个数x1,x2,…xn,其中每个数都可能取0,1,-2这三个数中的一个,且满足下列等式:x1+x2+…+xn=0,x12+x22+…+xn2=12,则x13+x23+…+xn3的值是 .
考点:规律型:数字的变化类
专题:
分析:先设有p个x取1,q个x取-2,根据x1+x2+…+xn=0,x12+x22+…+xn2=12可得出关于p,q的二元一次方程组,求出p,q的值,再把p,q及x的值代入x13+x23+…+xn3求解
解答:解:设有p个x取1,q个x取-2,有
,
解得
,
所以原式=4×13+2×(-2)3=-12.
故答案为:-12.
|
解得
|
所以原式=4×13+2×(-2)3=-12.
故答案为:-12.
点评:本题考查的是数字的变化类及解二元一次方程组,根据题意找出规律是解答此题的关键.

练习册系列答案
相关题目
已知一个三角形的两边长分别为6cm和3cm,则此三角形第三边的长可能是( )
| A、2cm | B、3cm |
| C、5cm | D、9cm |
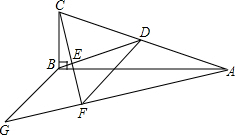 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过A作BD的平行线,交CE的延长线与点F,在AF的延长线上截取FG=BD,连接BG,DF.若AF=8,CF=6,则四边形BDFG的周长为多少?
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过A作BD的平行线,交CE的延长线与点F,在AF的延长线上截取FG=BD,连接BG,DF.若AF=8,CF=6,则四边形BDFG的周长为多少? 能伸缩的校门,它利用了四边形的一个性质是
能伸缩的校门,它利用了四边形的一个性质是