题目内容
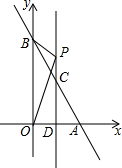 如图,在平面平面直角坐标系中,直线y=-2x+4交x轴于点A,交y轴与点B,点C是AB的中点,过点C作直线CD⊥x轴于点D,点P是直线CD上的动点.
如图,在平面平面直角坐标系中,直线y=-2x+4交x轴于点A,交y轴与点B,点C是AB的中点,过点C作直线CD⊥x轴于点D,点P是直线CD上的动点.(1)填空:线段OA的长为
(2)求点C的坐标;
(3)是否存在这样的点P,使△POB为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
考点:一次函数综合题
专题:
分析:(1)根据自变量与函数值的关系,函数值为零时,可得相应自变量的值;自变量为零时,可得相应的函数值;
(2)根据线段中点公式:线段两端点的横坐标的平均数是中点的横坐标,线段两端点的纵坐标的平均数是中点的纵坐标,可得答案;
(3)分类讨论:①当PO=PB时,②当PO=OB时,③当PB=OB时,可得关于a的方程,根据解方程,可得答案.
(2)根据线段中点公式:线段两端点的横坐标的平均数是中点的横坐标,线段两端点的纵坐标的平均数是中点的纵坐标,可得答案;
(3)分类讨论:①当PO=PB时,②当PO=OB时,③当PB=OB时,可得关于a的方程,根据解方程,可得答案.
解答:解:(1)当y=0时,-2x+4=0.解得x=2,即OA=2.
当x=0时,y=4,即OB=4,
故答案为:2,4;
(2)A(2,0),B(0,4),由中点坐标,得C点的横坐标为
=1,纵坐标为
=2,
即C(1,2);
(3)存在这样的点P,使△POB为等腰三角形,理由如下:
设P(1,a),
①当PO=PB时,平方,得PO2=PB2,即1+a2=12+(a-4)2,
化简,得8a=16.解得a=2,即P1(1,2);
②当PO=OB时,平方,得PO2=OB2,即1+a2=42,
解得a=±
,即P2(1,
),P3(1,-
);
③当PB=OB时,平方,得
PB2=OB2,即1+(a-4)2=42,解得a=4±
,即P4(1,4+
),P5(1,4-
),
综上所述:存在这样的点P,使△POB为等腰三角形,P1(1,2);P2(1,
),P3(1,-
);P4(1,4+
),P5(1,4-
).
当x=0时,y=4,即OB=4,
故答案为:2,4;
(2)A(2,0),B(0,4),由中点坐标,得C点的横坐标为
| 2+0 |
| 2 |
| 0+4 |
| 2 |
即C(1,2);
(3)存在这样的点P,使△POB为等腰三角形,理由如下:
设P(1,a),
①当PO=PB时,平方,得PO2=PB2,即1+a2=12+(a-4)2,
化简,得8a=16.解得a=2,即P1(1,2);
②当PO=OB时,平方,得PO2=OB2,即1+a2=42,
解得a=±
| 15 |
| 15 |
| 15 |
③当PB=OB时,平方,得
PB2=OB2,即1+(a-4)2=42,解得a=4±
| 15 |
| 15 |
| 15 |
综上所述:存在这样的点P,使△POB为等腰三角形,P1(1,2);P2(1,
| 15 |
| 15 |
| 15 |
| 15 |
点评:本题考查了一次函数综合题,(1)利用了函数值与自变量的关系,(2)利用了线段中点公式:线段两端点的横坐标的平均数是中点的横坐标,线段两端点的纵坐标的平均数是中点的纵坐标;(3)分类讨论是解题关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
如图,如果从半径为5cm的圆形纸片上剪去
圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),则这个圆锥的高为( )
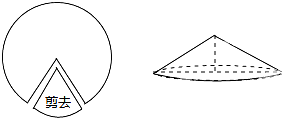
| 1 |
| 5 |

| A、1cm | ||
| B、3cm | ||
C、2
| ||
| D、4cm |
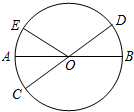 如图,AB,CD是⊙O的直径,
如图,AB,CD是⊙O的直径, |
| AE |
 |
| BD |
| A、32° | B、60° |
| C、68° | D、64° |
根据图中数字的规律,最后一个空格应填的数是( )

| A、738 | B、720 |
| C、550 | D、500 |
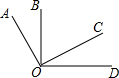 如图,OA⊥OC,OB⊥OD,①∠AOB=∠COD;②∠BOC+∠AOD=180°;③∠AOB+∠COD=90°;④图中小于平角的角有6个;其中正确的结论有几个( )
如图,OA⊥OC,OB⊥OD,①∠AOB=∠COD;②∠BOC+∠AOD=180°;③∠AOB+∠COD=90°;④图中小于平角的角有6个;其中正确的结论有几个( )| A、1个 | B、2个 | C、3个 | D、4个 |
在Rt△ABC中,如果各边的长度都缩小至原来的
,那么锐角A的各个三角函数值( )
| 1 |
| 4 |
A、都缩小
| ||
| B、都扩大4倍 | ||
| C、都不变 | ||
| D、无法确定 |
 如图是一个几何体从三个方向看所得到的形状图.
如图是一个几何体从三个方向看所得到的形状图.