题目内容
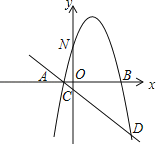
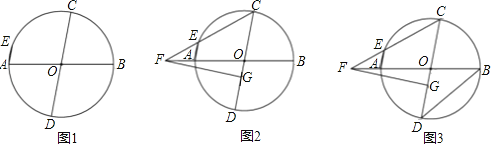
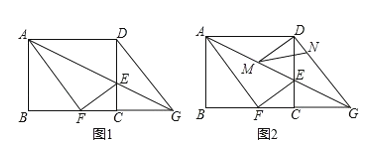
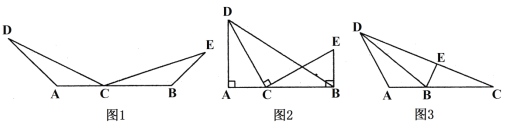
【题目】⑴如图1,点C在线段AB上,点D、E在直线AB同侧,∠A=∠DCE=∠CBE,DC=CE.求证:AC=BE.
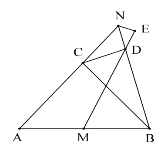
⑵如图2,点C在线段AB上,点D、E在直线AB同侧,∠A=∠DCE=∠CBE=90°.
①求证:![]() ;②连接BD,若∠ADC=∠ABD,AC=3,BC=
;②连接BD,若∠ADC=∠ABD,AC=3,BC=![]() ,求tan∠CDB的值;
,求tan∠CDB的值;
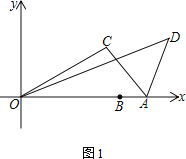
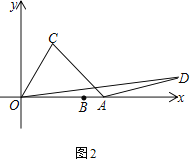
⑶如图3,在△ABD中,点C在AB边上,且∠ADC=∠ABD,点E在BD边上,连接CE,∠BCE+∠BAD=180°,AC=3,BC=![]() ,CE=
,CE=![]() ,直接写出
,直接写出![]() 的值.
的值.
【答案】(1)见解析;(2)①见解析;②![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用AAS证明![]() 可得AC=BE;
可得AC=BE;
(2)①先证明△DAC∽△CBE,再利用相似三角形的性质可得![]() ;
;
②根据∠A=∠DCE=∠CBE=90°,∠ADC=∠ABD,可推出△ADC∽△ADB,从而求出相应的线段长度,得到tan∠CDB的值.
(3)根据∠ADC=∠ABD,可推出△ADC∽△ADB,从而得到AD的长,根据∠BCE+∠BAD=180°,以E为圆心,EC长为半径画弧,交BC于点H,连接EH,可得EH=EC,∠EHC=∠ECB=∠ADC+∠DCA,可得△BEH∽△ADC,则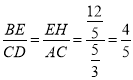 .
.
(1)证明:如图1,
![]() ,
,![]()
又![]() ,
,![]()
![]()
又![]()
![]()
![]()
(2)①证明:∵∠DCA+∠DCE+∠ECB=180°,
∠DCA+∠A+∠CDA=180°,∠A=∠DCE,
∴∠ADC=∠ECB,
∵∠A=∠B,
∴△DAC∽△CBE,
![]()
②如图2,
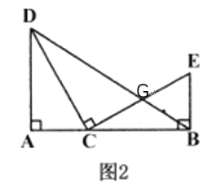
∵∠ADC=∠DBA,∠A=∠A,
∴△ADC∽△ABD,
![]()
AB=AC+BC=![]()
∴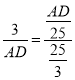
解得AD=5,
![]()
设∠DBA=∠CDA=α,
∴∠CDG=90-2α,
∴∠CGD=2α,
∴∠GCB=∠GBC=α,
∴CG=GB,
设CG=GB=x,
![]()
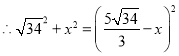
解得![]()
![]()
(3)如图3,
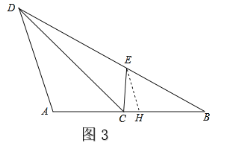
∵∠ADC=∠B,∠A=∠A,
∴△ADC∽△ADB,
![]()
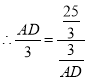
解得AD=5,
∵∠BCE+∠BAD=180°,∠ADC+∠DCA+∠BAD=180°,
∴∠ADC+∠DCA=∠BCE,
以E为圆心,EC长为半径画弧,交BC于点H,连接EH,
∴EH=EC,∠EHC=∠ECB=∠ADC+∠DCA,
∵∠B=∠ADC,
∴∠BEH=∠ACD,
∴△BEH∽△ADC,
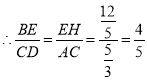
故答案为:![]()

 名题金卷系列答案
名题金卷系列答案【题目】随着中央电视台《朗读者》节目的播出,“朗读”为越来越多的同学所喜爱,西宁市某中学计划在全校开展“朗读”活动,为了了解同学们对这项活动的参与态度,随机对部分学生进行了一次调查,调查结果整理后,将这部分同学的态度划分为四个类别:![]() .积极参与,
.积极参与,![]() .一定参与,
.一定参与,![]() .可以参与,
.可以参与,![]() .不参与.根据调查结果制作了如下不完整的统计表和统计图.
.不参与.根据调查结果制作了如下不完整的统计表和统计图.
学生参与“朗读”的态度统计表
类别 | 人数 | 所占百分比 |
| 18 |
|
| 20 |
|
|
|
|
| 4 |
|
合计 |
|
|
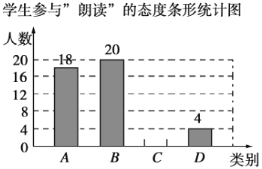
请你根据以上信息,解答下列问题:
(1)![]() ______,
______,![]() ______,并将条形统计图补充完整;
______,并将条形统计图补充完整;
(2)该校有1500名学生,如果“不参与”的人数不超过150人时,“朗读”活动可以顺利开展,通过计算分析这次活动能否顺利开展?
(3)“朗读”活动中,九年级一班比较优秀的四名同学恰好是两男两女,从中随机选取两人在班级进行朗读示范,试用画树状图法或列表法求所选两人都是女生的概率,并列出所有等可能的结果.