题目内容
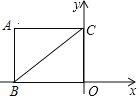
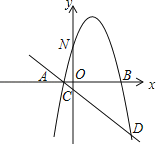
【题目】如图,抛物线![]() 与x轴交于A、B两点(A在B的左侧),与y轴交于点N,过A点的直线l:
与x轴交于A、B两点(A在B的左侧),与y轴交于点N,过A点的直线l:![]() 与y轴交于点C,与抛物线
与y轴交于点C,与抛物线![]() 的另一个交点为D,已知
的另一个交点为D,已知![]() ,P点为抛物线
,P点为抛物线![]() 上一动点(不与A、D重合).
上一动点(不与A、D重合).
(1)求抛物线和直线l的解析式;
(2)当点P在直线l上方的抛物线上时,过P点作PE∥x轴交直线l于点E,作![]() 轴交直线l于点F,求
轴交直线l于点F,求![]() 的最大值;
的最大值;
(3)设M为直线l上的点,探究是否存在点M,使得以点N、C,M、P为顶点的四边形为平行四边形?若存在,求出点M的坐标;若不存在,请说明理由.
【答案】(1)![]() ,直线l的表达式为:
,直线l的表达式为:![]() ;(2)
;(2)![]() 最大值:18;(3)存在,P的坐标为:
最大值:18;(3)存在,P的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.
【解析】
(1)将点A、D的坐标分别代入直线表达式、抛物线的表达式,即可求解;
(2)![]() ,即可求解;
,即可求解;
(3)分NC是平行四边形的一条边、NC是平行四边形的对角线,两种情况分别求解即可.
解:(1)将点A、D的坐标代入直线表达式得:![]() ,解得:
,解得:![]() ,
,
故直线l的表达式为:![]() ,
,
将点A、D的坐标代入抛物线表达式,
同理可得抛物线的表达式为:![]() ;
;
(2)直线l的表达式为:![]() ,则直线l与x轴的夹角为
,则直线l与x轴的夹角为![]() ,
,
即:则![]() ,
,
设点P坐标为![]() 、则点
、则点![]() ,
,
![]()
![]() ,故
,故![]() 有最大值,
有最大值,
当![]() 时,其最大值为18;
时,其最大值为18;
(3)![]() ,
,
①当NC是平行四边形的一条边时,
设点P坐标为![]() 、则点
、则点![]() ,
,
由题意得:![]() ,即:
,即:![]() ,
,
解得![]() 或0或4(舍去0),
或0或4(舍去0),
则点P坐标为![]() 或
或![]() 或
或![]() ;
;
②当NC是平行四边形的对角线时,
则NC的中点坐标为![]() ,
,
设点P坐标为![]() 、则点
、则点![]() ,
,
N、C,M、P为顶点的四边形为平行四边形,则NC的中点即为PM中点,
即:![]() ,
,
解得:![]() 或
或![]() (舍去0),
(舍去0),
故点![]() ;
;
故点P的坐标为:![]() 或
或![]() 或
或![]() 或
或![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】已知一个二次函数图象上部分点的横坐标![]() 与纵坐标
与纵坐标![]() 的对应值如表所示:
的对应值如表所示:
| … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
| … | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | … |
(1)求这个二次函数的表达式;
(2)在给定的平面直角坐标系中画出这个二次函数的图象;
(3)当![]() 时,直接写出
时,直接写出![]() 的取值范围.
的取值范围.
【题目】为了了解学生每月的零用钱情况,从甲、乙、丙三个学校各随机抽取200名学生,调查了他们的零用钱情况(单位:元)具体情况如下:
学校频数零用钱 | 100≤x<200 | 200≤x<300 | 300≤x<400 | 400≤x<500 | 500以上 | 合计 |
甲 | 5 | 35 | 150 | 8 | 2 | 200 |
乙 | 16 | 54 | 68 | 52 | 10 | 200 |
丙 | 0 | 10 | 40 | 70 | 80 | 200 |
在调查过程中,从__(填“甲”,“乙”或“丙”)校随机抽取学生,抽到的学生“零用钱不低于300元”的可能性最大.