题目内容
16.指出下列二次函数图象的开口方向、对称轴和顶点坐标.(1)y=2(x-3)2-5;
(2)y=-0.5(x+1)2;
(3)y=-$\frac{3}{4}$x2-1;
(4)y=2(x-2)2+5;
(5)y=0.5(x+4)2+2;
(6)y=-$\frac{3}{4}$(x-3)2.
分析 由抛物线的顶点式y=a(x-h)2+k,可知a>0,抛物线开口向上,a<0,抛物线开口向下;对称轴是直线x=h;顶点坐标是(h,k);利用这个结论即可确定各二次函数图象的开口方向、对称轴和顶点坐标.
解答 解:(1)由y=2(x-3)2-5,
可知,二次项系数为2>0,
所以抛物线开口向上,对称轴为直线x=3,
顶点坐标为(3,-5);
(2)由y=-0.5(x+1)2,
可知,二次项系数为-0.5<0,
所以抛物线开口向下,对称轴为直线x=-1,
顶点坐标为(-1,0);
(3)由y=-$\frac{3}{4}$x2-1,
可知,二次项系数为-$\frac{3}{4}$<0,
所以抛物线开口向下,对称轴为直线x=0,
顶点坐标为(0,-1);
(4)由y=2(x-2)2+5,
可知,二次项系数为2>0,
所以抛物线开口向上,对称轴为直线x=2,
顶点坐标为(2,5);
(5)由y=0.5(x+4)2+2,
可知,二次项系数为0.5>0,
所以抛物线开口向上,对称轴为直线x=-4,
顶点坐标为(-4,2);
(6)由y=-$\frac{3}{4}$(x-3)2,
可知,二次项系数为-$\frac{3}{4}$<0,
所以抛物线开口向下,对称轴为直线x=3,
顶点坐标为(3,0).
点评 本题考查由抛物线的顶点坐标式写出抛物线的开口方向,对称轴方程和顶点坐标,比较容易.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
7.一枚炮弹射出x秒后的高度为y米,且y与x之间的关系为y=ax2+bx+c(a≠0),若此炮弹在第3.2秒与第5.8秒时的高度相等,则在下列时间中炮弹所在高度最高的是( )
| A. | 第3.3s | B. | 第4.3s | C. | 第5.2s | D. | 第4.6s |
 画出△ABC关于x轴和y轴对称的图形△A1B1C1和△A2B2C2,并指出△A1B1C1和△A2B2C2的顶点坐标.
画出△ABC关于x轴和y轴对称的图形△A1B1C1和△A2B2C2,并指出△A1B1C1和△A2B2C2的顶点坐标.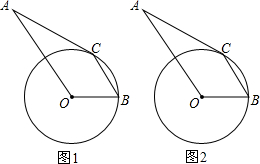 A为⊙O外一点,AC切⊙O于C,BC∥AO.
A为⊙O外一点,AC切⊙O于C,BC∥AO.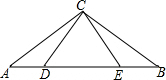 已知:如图,AC=BC,CD=CE,AC⊥EC于C,BC⊥DC于C,求证:AD=BE.
已知:如图,AC=BC,CD=CE,AC⊥EC于C,BC⊥DC于C,求证:AD=BE.