题目内容
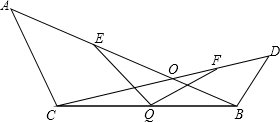 如图,已知:AB、CD交于点O,CA=CO,BO=BD,点Q是BC的中点,点E,F分别是OA,OD的中点,连接QE、QF,试探讨QE、QF的大小关系,并说明理由.
如图,已知:AB、CD交于点O,CA=CO,BO=BD,点Q是BC的中点,点E,F分别是OA,OD的中点,连接QE、QF,试探讨QE、QF的大小关系,并说明理由.考点:直角三角形斜边上的中线,等腰三角形的判定与性质
专题:
分析:连接CE、BF,根据等腰三角形三线合一的性质可得CE⊥AB,BF⊥CD,再根据直角三角形斜边上的中线等于斜边的一半可得QE=
BC,QF=
BC,从而得解.
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:QE=QF.理由如下:
解:QE=QF.理由如下:
如图,连接CE、BF,
∵CA=CO,BO=BD,点E,F分别是OA,OD的中点,
∴CE⊥AB,BF⊥CD,
∵点Q是BC的中点,
∴QE=
BC,QF=
BC,
∴QE=QF.
 解:QE=QF.理由如下:
解:QE=QF.理由如下:如图,连接CE、BF,
∵CA=CO,BO=BD,点E,F分别是OA,OD的中点,
∴CE⊥AB,BF⊥CD,
∵点Q是BC的中点,
∴QE=
| 1 |
| 2 |
| 1 |
| 2 |
∴QE=QF.
点评:本题考查了等腰三角形的性质,直角三角形斜边上的中线等于斜边的一半的性质,熟记性质并作辅助线构造出直角三角形是解题的关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
下列语句:
①无理数都是无限小数;
②实数的平方根有两个,而立方根只有一个;
③过一点有且只有一条直线与已知直线平行.
其中( )
①无理数都是无限小数;
②实数的平方根有两个,而立方根只有一个;
③过一点有且只有一条直线与已知直线平行.
其中( )
| A、①、②是真命题 |
| B、②、③是真命题 |
| C、①、③是真命题 |
| D、以上结论都不对 |
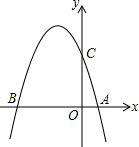 如图,抛物线y=-x2+bx+c与x轴交于A(1,0)、B(-4,0)两点,交y轴与C点.
如图,抛物线y=-x2+bx+c与x轴交于A(1,0)、B(-4,0)两点,交y轴与C点.