题目内容
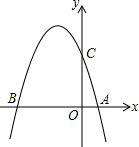 如图,抛物线y=-x2+bx+c与x轴交于A(1,0)、B(-4,0)两点,交y轴与C点.
如图,抛物线y=-x2+bx+c与x轴交于A(1,0)、B(-4,0)两点,交y轴与C点.(1)求该抛物线的解析式;
(2)在该抛物线位于第二象限的部分上是否存在点D,使得△DBC的面积S最大?若存在,求出点D的坐标;若不存在,请说明理由;
(3)设抛物线的顶点为点F,连接线段CF,连接直线BC,请问能否在直线BC上找到一个点M,在抛物线上找到一个点N,使得C、F、M、N四点组成的四边形为平行四边形?若存在,请写出点M和点N的坐标;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)根据题意可知,将点A、B代入函数解析式,列得方程组即可求得b、c的值,求得函数解析式;
(2)存在,设出点D的坐标,将△DBC的面积表示成二次函数,根据二次函数最值的方法即可求得点D的坐标;
(3)根据平行四边形的性质,分①CF是边;②CF是对角线.
(2)存在,设出点D的坐标,将△DBC的面积表示成二次函数,根据二次函数最值的方法即可求得点D的坐标;
(3)根据平行四边形的性质,分①CF是边;②CF是对角线.
解答:解:(1)将A(1,0),B(-4,0)代入y=-x2+bx+c中得
,
解得
.
所以抛物线解析式为:y=-x2-3x+4;
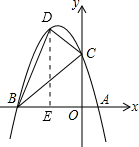 (2)在该抛物线位于第二象限的部分上是否存在点D,使得△DBC的面积S最大.理由如下:
(2)在该抛物线位于第二象限的部分上是否存在点D,使得△DBC的面积S最大.理由如下:
设D点坐标为(x,-x2-3x+4)(-4<x<0).如图,过D点作DE⊥x轴于点E.
∵S△DBC=S四边形BDCO-S△BOC=S四边形BDCO-
×4×4=S四边形BDCO-8,
若S四边形BDCO有最大值,则S△DBC就最大,
∴S四边形BDCO=S△BDE+S直角梯形DEOC
=
BE•DE+
OE(DE+OC)
=
(x+4)(-x2-3x+4)+
(-x)(-x2-3x+4+4)
=-2x2-8x+8
=-2(x+2)2+16,
当x=-2时,S四边形BDCO最大值=16.
∴S△BDC最大值=16-8=8.
当x=-2时,-x2-3x+4=-(-2)2-3×(-2)+4=6,
∴点D坐标为(-2,6);
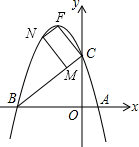 (3)能够在直线BC上找到一个点M,在抛物线上找到一个点N,使得C、F、M、N四点组成的四边形为平行四边形.理由如下:
(3)能够在直线BC上找到一个点M,在抛物线上找到一个点N,使得C、F、M、N四点组成的四边形为平行四边形.理由如下:
∵y=-x2-3x+4=-(x+
)2+
,
∴顶点F的坐标为(-
,
).
∵B(-4,0),C(0,4),
∴直线BC的解析式为y=x+4.
分两种情况:①CF是边.
如图,过点F作FN∥BC,交抛物线于点N,设直线FN的解析式为y=x+m,
把F(-
,
)代入,得-
+m=
,
解得m=
,
∴直线FN的解析式为y=x+
.
由
,解得
或
,
∴点N的坐标为(-
,
).
∵F(-
,
),N(-
,
),
∴FN2=(-
+
)2+(
-
)2=2.
∵四边形CFNM是平行四边形,
∴CM=FN.
设M点的坐标为(x,x+4),则
CM2=x2+(x+4-4)2=2x2=2,
解得x=±1,
 x=1不合题意舍去,
x=1不合题意舍去,
∴x=-1,
∴M点的坐标为(-1,3);
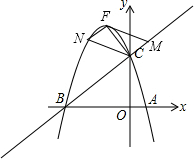
②CF是对角线.如图.
∵四边形CMFN是平行四边形,
∴FN∥BC,CM=FN.
由①可知,点N的坐标为(-
,
),M点的横坐标为1,
当x=1时,x+4=5,
∴M点的坐标为(1,5).
综上所述,符合条件的点M的坐标为(-1,3)或(1,5),点N的坐标为(-
,
).
|
解得
|
所以抛物线解析式为:y=-x2-3x+4;
 (2)在该抛物线位于第二象限的部分上是否存在点D,使得△DBC的面积S最大.理由如下:
(2)在该抛物线位于第二象限的部分上是否存在点D,使得△DBC的面积S最大.理由如下:设D点坐标为(x,-x2-3x+4)(-4<x<0).如图,过D点作DE⊥x轴于点E.
∵S△DBC=S四边形BDCO-S△BOC=S四边形BDCO-
| 1 |
| 2 |
若S四边形BDCO有最大值,则S△DBC就最大,
∴S四边形BDCO=S△BDE+S直角梯形DEOC
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
=-2x2-8x+8
=-2(x+2)2+16,
当x=-2时,S四边形BDCO最大值=16.
∴S△BDC最大值=16-8=8.
当x=-2时,-x2-3x+4=-(-2)2-3×(-2)+4=6,
∴点D坐标为(-2,6);
 (3)能够在直线BC上找到一个点M,在抛物线上找到一个点N,使得C、F、M、N四点组成的四边形为平行四边形.理由如下:
(3)能够在直线BC上找到一个点M,在抛物线上找到一个点N,使得C、F、M、N四点组成的四边形为平行四边形.理由如下:∵y=-x2-3x+4=-(x+
| 3 |
| 2 |
| 25 |
| 4 |
∴顶点F的坐标为(-
| 3 |
| 2 |
| 25 |
| 4 |
∵B(-4,0),C(0,4),
∴直线BC的解析式为y=x+4.
分两种情况:①CF是边.
如图,过点F作FN∥BC,交抛物线于点N,设直线FN的解析式为y=x+m,
把F(-
| 3 |
| 2 |
| 25 |
| 4 |
| 3 |
| 2 |
| 25 |
| 4 |
解得m=
| 31 |
| 4 |
∴直线FN的解析式为y=x+
| 31 |
| 4 |
由
|
|
|
∴点N的坐标为(-
| 5 |
| 2 |
| 21 |
| 4 |
∵F(-
| 3 |
| 2 |
| 25 |
| 4 |
| 5 |
| 2 |
| 21 |
| 4 |
∴FN2=(-
| 3 |
| 2 |
| 5 |
| 2 |
| 25 |
| 4 |
| 21 |
| 4 |
∵四边形CFNM是平行四边形,
∴CM=FN.
设M点的坐标为(x,x+4),则
CM2=x2+(x+4-4)2=2x2=2,
解得x=±1,
 x=1不合题意舍去,
x=1不合题意舍去,∴x=-1,
∴M点的坐标为(-1,3);
②CF是对角线.如图.
∵四边形CMFN是平行四边形,
∴FN∥BC,CM=FN.
由①可知,点N的坐标为(-
| 5 |
| 2 |
| 21 |
| 4 |
当x=1时,x+4=5,
∴M点的坐标为(1,5).
综上所述,符合条件的点M的坐标为(-1,3)或(1,5),点N的坐标为(-
| 5 |
| 2 |
| 21 |
| 4 |
点评:本题是二次函数综合题型,其中涉及到运用待定系数法求二次函数、一次函数的解析式,三角形的面积,二次函数的最值求法,两函数交点坐标的求法,平行四边形的对边平行且相等的性质等知识,难点在于(3)要分情况讨论.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
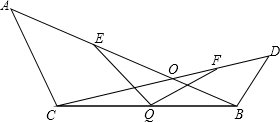 如图,已知:AB、CD交于点O,CA=CO,BO=BD,点Q是BC的中点,点E,F分别是OA,OD的中点,连接QE、QF,试探讨QE、QF的大小关系,并说明理由.
如图,已知:AB、CD交于点O,CA=CO,BO=BD,点Q是BC的中点,点E,F分别是OA,OD的中点,连接QE、QF,试探讨QE、QF的大小关系,并说明理由.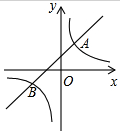 如图,直线y=x+2与双曲线y=
如图,直线y=x+2与双曲线y= 如图,EF∥AD,∠1=∠2.求证:DG∥AB.
如图,EF∥AD,∠1=∠2.求证:DG∥AB.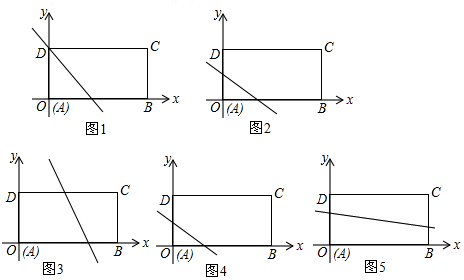
 右图为手的示意图,在各个手指间标记字母 A,B,C,D.请你按图中箭头所指方向(即 A→B→C→D→C→B→A→B→C→…的方式)从 A 开始数连续的正整数 1,2,3,4,…,当字母C第2n+1次出现时(n为正整数),恰好数到的数是
右图为手的示意图,在各个手指间标记字母 A,B,C,D.请你按图中箭头所指方向(即 A→B→C→D→C→B→A→B→C→…的方式)从 A 开始数连续的正整数 1,2,3,4,…,当字母C第2n+1次出现时(n为正整数),恰好数到的数是