题目内容
如图，已知DE⊥DB于D，∠ADE=60°，DC是∠ADB的平分线，则∠ADC=________°．
15
分析：由垂直先得90°，再求∠ADB的度数，根据角平分线的定义可得∠ADC的度数．
解答：∵DE⊥DB，
∴∠BDE=90°，
∴∠ADB=90°-∠ADE=30°；
∵DC是∠ADB的平分线，
∴∠ADC=
∠ADB=15°．
点评：注意由垂直可得90°，由90°可得垂直．
分析：由垂直先得90°，再求∠ADB的度数，根据角平分线的定义可得∠ADC的度数．
解答：∵DE⊥DB，
∴∠BDE=90°，
∴∠ADB=90°-∠ADE=30°；
∵DC是∠ADB的平分线，
∴∠ADC=
∠ADB=15°．点评：注意由垂直可得90°，由90°可得垂直．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
如图，已知DE∥BC，AD=5，DB=3，BC=99，则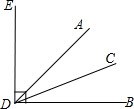
如图，已知DE⊥DB于D，∠ADE=60°，DC是∠ADB的平分线，则∠ADC=
如图：已知DE∥BC，AD=1，DB=2，DE=3，则BC=
如图，已知DE∥BC，且DB=2AD，则以下说法中正确的个数有（ ）