题目内容
 如图,双曲线y=
如图,双曲线y= 上两点A、B,xB=2xA=2,AF∥x轴,AC∥OF交OB于E,且S四边形ABOF=
上两点A、B,xB=2xA=2,AF∥x轴,AC∥OF交OB于E,且S四边形ABOF= ,则k=________.
,则k=________.
1.2
分析:首先过点B作BM⊥x轴于点M,求出AC=k,BM= ,由S五边形AFOMB=S四边形ABOF+S△OBM=
,由S五边形AFOMB=S四边形ABOF+S△OBM= +
+ ,进而得出S五边形AFOMB=S四边形AFOC+S四边形ACMB=
,进而得出S五边形AFOMB=S四边形AFOC+S四边形ACMB= k,进而求出即可.
k,进而求出即可.
解答: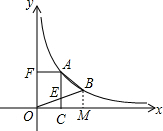 解:过点B作BM⊥x轴于点M,
解:过点B作BM⊥x轴于点M,
∵双曲线y= 上两点A、B,xB=2xA=2,
上两点A、B,xB=2xA=2,
∴B点横坐标为:2,纵坐标为: ,
,
A点横坐标为:1,纵坐标为:k,
∴AC=k,BM= ,
,
∵S四边形ABOF= ,
,
S△OBM= ×BM×MO=
×BM×MO= ,
,
∴S五边形AFOMB=S四边形ABOF+S△OBM= +
+ ,
,
∵S五边形AFOMB=S四边形AFOC+S四边形ACMB=AF×AC+ (AC+BM)×MC=k+
(AC+BM)×MC=k+ k=
k= k=
k= +
+ ,
,
∴解得:k=1.2,
故答案为:1.2.
点评:此题主要考查了反比例函数系数k的几何意义,根据已知得出S五边形AFOMB=S四边形ABOF+S△OBM=S四边形AFOC+S四边形ACMB是解题关键.
分析:首先过点B作BM⊥x轴于点M,求出AC=k,BM=
 ,由S五边形AFOMB=S四边形ABOF+S△OBM=
,由S五边形AFOMB=S四边形ABOF+S△OBM= +
+ ,进而得出S五边形AFOMB=S四边形AFOC+S四边形ACMB=
,进而得出S五边形AFOMB=S四边形AFOC+S四边形ACMB= k,进而求出即可.
k,进而求出即可.解答:
 解:过点B作BM⊥x轴于点M,
解:过点B作BM⊥x轴于点M,∵双曲线y=
 上两点A、B,xB=2xA=2,
上两点A、B,xB=2xA=2,∴B点横坐标为:2,纵坐标为:
 ,
,A点横坐标为:1,纵坐标为:k,
∴AC=k,BM=
 ,
,∵S四边形ABOF=
 ,
,S△OBM=
 ×BM×MO=
×BM×MO= ,
,∴S五边形AFOMB=S四边形ABOF+S△OBM=
 +
+ ,
,∵S五边形AFOMB=S四边形AFOC+S四边形ACMB=AF×AC+
 (AC+BM)×MC=k+
(AC+BM)×MC=k+ k=
k= k=
k= +
+ ,
,∴解得:k=1.2,
故答案为:1.2.
点评:此题主要考查了反比例函数系数k的几何意义,根据已知得出S五边形AFOMB=S四边形ABOF+S△OBM=S四边形AFOC+S四边形ACMB是解题关键.

练习册系列答案
相关题目
 x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+
x,y轴平行,纸板的另两个顶点A,B恰好是直线y=kx+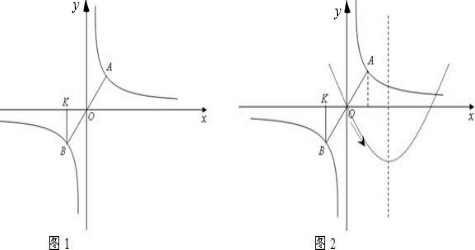
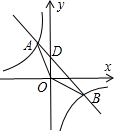 如图.反比例函数
如图.反比例函数
 经过
经过 的两个顶点
的两个顶点 、
、 轴,连接
轴,连接 ,将
,将 翻折后得到
翻折后得到 ,点
,点 刚好落在线段
刚好落在线段 ,
, 轴负半轴的夹角,若
轴负半轴的夹角,若 的值为
。
的值为
。