题目内容
 如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.AD=5cm,DE=3cm,BE的长度是
如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D.AD=5cm,DE=3cm,BE的长度是考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:求出∠E=∠ADC=∠ACB=90°,∠EBC=∠ACD,根据AAS证出△BEC≌△CDA,根据全等三角形的性质得出AD=CE=5cm,BE=CD即可.
解答:解:∵BE⊥CE,AD⊥CE,
∴∠E=∠ADC=∠ACB=90°,
∴∠EBC+∠BCE=90°,∠BCE+∠ACD=90°,
∴∠EBC=∠ACD,
在△BEC和△CDA中,
,
∴△BEC≌△CDA(AAS),
∴AD=CE=5cm,BE=CD,
∵DE=3cm,
∴BE=CD=5-3=2cm.
故答案为:2cm.
∴∠E=∠ADC=∠ACB=90°,
∴∠EBC+∠BCE=90°,∠BCE+∠ACD=90°,
∴∠EBC=∠ACD,
在△BEC和△CDA中,
|
∴△BEC≌△CDA(AAS),
∴AD=CE=5cm,BE=CD,
∵DE=3cm,
∴BE=CD=5-3=2cm.
故答案为:2cm.
点评:本题考查了全等三角形的性质和判定的应用,解此题的关键是推出△BEC≌△CDA,注意:全等三角形的对应边相等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 利用网格线作图:
利用网格线作图: 在正方形ABCD中,E是AB的中点,AF=
在正方形ABCD中,E是AB的中点,AF=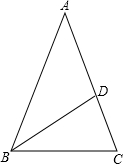 如图,在△ABC中,AB=AC,BD平分∠ABC,若∠BDC=84°.求∠A的度数.
如图,在△ABC中,AB=AC,BD平分∠ABC,若∠BDC=84°.求∠A的度数.
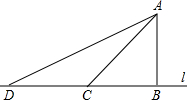 校车安全是当今社会关注的重大问题,安全隐患主要是超速和超载,某中学数学活动小组设计了如下检测公路上行驶的汽车速度实验:先在公路旁边选取一点A,再在笔直的车道L上确定点B,使AB与L垂直,测得AB=21米,在L上点B的同侧取点C、D,使∠ADB=30°,∠ACB=60°.
校车安全是当今社会关注的重大问题,安全隐患主要是超速和超载,某中学数学活动小组设计了如下检测公路上行驶的汽车速度实验:先在公路旁边选取一点A,再在笔直的车道L上确定点B,使AB与L垂直,测得AB=21米,在L上点B的同侧取点C、D,使∠ADB=30°,∠ACB=60°.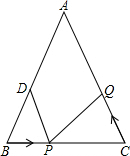 如图,在△ABC中,∠B=∠C,AB=10cm,点D为AB的中点.点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
如图,在△ABC中,∠B=∠C,AB=10cm,点D为AB的中点.点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.