题目内容
 如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有以下结论:①CD=ED,②AC+BE=AB,③∠BDE=∠BAC,④AD平分∠CDE,⑤S△ACD=S△ADE,其中正确的序号是
如图,在△ABC中,∠C=90°,AD平分∠BAC,DE⊥AB于E,有以下结论:①CD=ED,②AC+BE=AB,③∠BDE=∠BAC,④AD平分∠CDE,⑤S△ACD=S△ADE,其中正确的序号是考点:角平分线的性质
专题:
分析:根据角平分线上的点到角的两边距离相等可得CD=DE,然后利用“HL”证明Rt△ACD和Rt△AED全等,根据全等三角形对应边相等可得AE=AC,全等三角形对应角相等可得∠ADC=∠ADE,然后对各小题分析判断即可得解.
解答:解:∵∠C=90°,AD平分∠BAC,DE⊥AB,
∴CD=DE,故①正确;
在Rt△ACD和Rt△AED中,
,
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC,∠BDE=∠BAC,故③正确;
∴AC+BE=AE+BE=AB,故②正确;
AD平分∠CDE,故④正确;
S△ACD=S△ADE,故⑤正确;
综上所述,正确的序号是①②③④⑤.
故答案为:①②③④⑤.
∴CD=DE,故①正确;
在Rt△ACD和Rt△AED中,
|
∴Rt△ACD≌Rt△AED(HL),
∴AE=AC,∠BDE=∠BAC,故③正确;
∴AC+BE=AE+BE=AB,故②正确;
AD平分∠CDE,故④正确;
S△ACD=S△ADE,故⑤正确;
综上所述,正确的序号是①②③④⑤.
故答案为:①②③④⑤.
点评:本题考查了角平分线上的点到角的两边距离相等的性质,全等三角形的判定与性质,熟记性质并求出三角形全等是解题的关键.

练习册系列答案
相关题目
某水坝的坡度i=1:
,水平长度AB=10
米,则坝的高度为( )
| 3 |
| 3 |
| A、10米 | ||
| B、20米 | ||
| C、40米 | ||
D、10
|
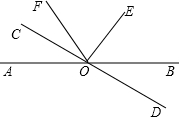 如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=28°,求∠BOD的度数.
如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=28°,求∠BOD的度数. 如图,△ABC内接于⊙O,∠BAC=60°,弦BC=2
如图,△ABC内接于⊙O,∠BAC=60°,弦BC=2 如图所示,阴影部分是一个半圆,求这个半圆的面积(精确到0.1cm2)
如图所示,阴影部分是一个半圆,求这个半圆的面积(精确到0.1cm2)