Question

17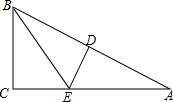．如图，在△ABC中，点D在AB上，DE⊥AB于D，交AC于E，BC=BD，DE=CE．
（1）求证：∠C=90°；
（2）若点D是AB的中点，求∠A．

Answer 1

分析 （1）利用“边边边”证明△BCE和△BDE全等，根据全等三角形对应角相等可得∠C=∠BDE，再根据垂直的定义证明即可；
（2）根据全等三角形对应角相等可得∠CBE=∠DBE，根据等边对等角可得∠DBE=∠A，然后根据直角三角形两锐角互余列式计算即可得解．

解答 （1）证明：在△BCE和△BDE中，
$\left\{\begin{array}{l}{BC=BD}\\{DE=CE}\\{BE=BE}\end{array}\right.$，
∴△BCE≌△BDE（SSS），
∴∠C=∠BDE，
∵DE⊥AB，
∴∠BDE=90°，
∴∠C=90°；

（2）解：∵△BCE≌△BDE，
∴∠CBE=∠DBE，
∵点D是AB的中点，DE⊥AB，
∴AE=BE，
∴∠DBE=∠A，
∴∠ABC=2∠A，
在Rt△ABC中，∠A+∠ABC=90°，
∴∠A+2∠A=90°，
解得∠A=30°．

点评 本题考查了全等三角形的判定与性质，等边对等角的性质，直角三角形两锐角互余的性质，熟练掌握三角形全等的判断方法并准确确定出全等三角形是解题的关键．