题目内容
4. 如图,在△ABC中,AB=AC,以AB为直径的O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.
如图,在△ABC中,AB=AC,以AB为直径的O交BC于点D,过点D作EF⊥AC于点E,交AB的延长线于点F.(1)判断直线DE与⊙O的位置关系,并说明理由;
(2)如果AB=5,BC=6,求DE的长.
分析 (1)连接AD,OD,根据已知条件证得OD⊥DE即可;
(2)根据勾股定理计算即可.
解答 解:(1)相切,理由如下:
连接AD,OD,
∵AB为⊙O的直径,
∴∠ADB=90°.
∴AD⊥BC.
∵AB=AC,
∴CD=BD=$\frac{1}{2}$BC.
∵OA=OB,
∴OD∥AC.
∴∠ODE=∠CED.
∵DE⊥AC,
∴∠ODE=∠CED=90°.
∴OD⊥DE.
∴DE与⊙O相切.
(2)由(1)知∠ADC=90°,
∴在Rt△ADC中,由勾股定理 得
AD=$\sqrt{A{C}^{2}-(\frac{1}{2}BC)^{2}}=\sqrt{{5}^{2}-(\frac{1}{2}×6)^{2}}$=4.
∵SACD=$\frac{1}{2}$AD•CD=$\frac{1}{2}$AC•DE,
∴$\frac{1}{2}$×4×3=$\frac{1}{2}$×5DE.
∴DE=$\frac{12}{5}$.
点评 本题考查了切线的判定,连接OD,证得OD⊥DE是解题关键.

练习册系列答案
相关题目
15.在平面直角坐标系中,点P(3,-1)关于x轴对称的点的坐标是( )
| A. | (-3,-1) | B. | (-3,1) | C. | (-1,3) | D. | (3,1) |
12.我市某中学九年级学生对市民“创建精神文明城市”知晓率采取随机抽样的方法进行问卷调查,问卷调查的结果划分为“非常了解”、“比较了解”、“基本了解”、“不太了解“、“从未听说”五个等级,统计后的数据整理如下表:
(1)表中m的值为0.3;
(2)根据表中的数据计算等级为“非常了解”的频数在扇形统计图中所对应扇形的圆心角的度数;
(3)根据上述统计结果,请你对政府相关部门提出一句话建议.
| 等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 | 从未听说 |
| 频数 | 40 | 60 | 48 | 36 | 16 |
| 频率 | 0.2 | m | 0.24 | 0.18 | 0.08 |
(2)根据表中的数据计算等级为“非常了解”的频数在扇形统计图中所对应扇形的圆心角的度数;
(3)根据上述统计结果,请你对政府相关部门提出一句话建议.
 一个能储水30升的电热水器,安装有一个进水管和一个出水管,进出水管每单位时间内进出的水量各自是一个定值.设从某时刻开始的4分钟内只补充进水而不出水,在随后的8分钟内出水的同时补充进水,得到容器中剩余水量y(升)与时间x(分)之间的函数关系如图所示.根据图象信息回答下列问题:
一个能储水30升的电热水器,安装有一个进水管和一个出水管,进出水管每单位时间内进出的水量各自是一个定值.设从某时刻开始的4分钟内只补充进水而不出水,在随后的8分钟内出水的同时补充进水,得到容器中剩余水量y(升)与时间x(分)之间的函数关系如图所示.根据图象信息回答下列问题: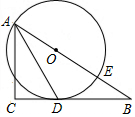 如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD.
如图,已知△ABC为直角三角形,∠C=90°,边BC是⊙0的切线,切点为D,AB经过圆心O并与圆相交于点E,连接AD. 数学活动课上,同学们正在讨论一道习题:
数学活动课上,同学们正在讨论一道习题: 如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,CO的延长线交⊙O于点E,BA,ED的延长线交于点F.
如图,AB为⊙O的直径,$\widehat{CB}$=$\widehat{CD}$,CO的延长线交⊙O于点E,BA,ED的延长线交于点F.