题目内容
18．
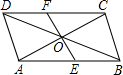如图，在?ABCD中，对角线AC，BD交于点O，EF是过点O的一条直线，交AB于点E，交DC于点F．请写出图中的一对全等三角形是△DOF≌△BOE．
分析 由BD、EF两两互相平分于点O，图形条件，∠DOF=∠BOE，可以判断△DOF≌△BOE；利用SAS，还可以判定其它全等三角形．
解答 解：∵BD、EF两两互相平分于点O，
∵在△DOF和△BOE中，
$\left\{\begin{array}{l}{OD=OB}\\{∠DOF=∠BOE}\\{OF=OE}\end{array}\right.$，
∴△DOF≌△BOE（SAS）．
故答案为：△DOF≌△BOE．
点评 本题考查了全等三角形的判定；利用图形中的对顶角是正确解答本题的关键．
练习册系列答案
相关题目
6．意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，其中从第三个数起，每一个数都等于它前面两个数的和．现以这组数中的各个数作为边长构造如下正方形：
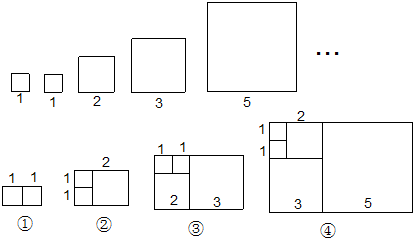
再分别依次从左到右取2个、3个、4个、5个正方形拼成矩形并记为①、②、③、④．相应矩形的周长如表所示：
若按此规律继续作矩形，则序号为⑥的矩形周长是68．
再分别依次从左到右取2个、3个、4个、5个正方形拼成矩形并记为①、②、③、④．相应矩形的周长如表所示：
| 序号 | ① | ② | ③ | ④ |
| 周长 | 6 | 10 | 16 | 26 |
13．
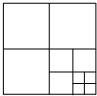如图，将一张正方形纸片剪成四个小正方形，然后将其中的一个正方形再剪成四个小正方形，再将其中的一个正方形剪成四个小正方形，如此继续下去，…，请你根据以上操作方法得到的正方形的个数的规律完成各题．
（1）将下表填写完整；
（2）an=3n+1（用含n的代数式表示）；
（3）按照上述方法，能否得到2015个正方形？如果能，请求出n；如果不能，请简述理由．
如图，将一张正方形纸片剪成四个小正方形，然后将其中的一个正方形再剪成四个小正方形，再将其中的一个正方形剪成四个小正方形，如此继续下去，…，请你根据以上操作方法得到的正方形的个数的规律完成各题．（1）将下表填写完整；
| 操作次数N | 1 | 2 | 3 | 4 | 5 | … | n |
| 正方形个数 | 4 | 7 | 10 | an |
（3）按照上述方法，能否得到2015个正方形？如果能，请求出n；如果不能，请简述理由．
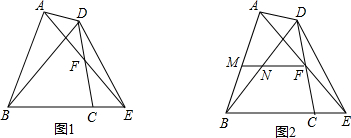
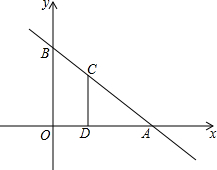如图，平面直角坐标系中，直线AB：y=-$\frac{3}{4}$x+3与x轴、y轴分别交于A（4，0）、B（0，3）两点，点C为线段AB上的一动点，过点C作CD⊥x轴于D．