题目内容
如图是一张直角三角形的纸片，两直角边AC＝6cm、BC＝8cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为（ ）
| A．4 cm | B．5 cm | C．6 cm | D．10 cm |
B
解析试题分析：先根据勾股定理求出AB的长，再由图形折叠的性质即可求得结果．
∵△ABC是直角三角形，两直角边AC=6cm、BC=8cm，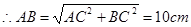
，
∵△ADE由△BDE折叠而成，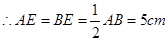
，
故选B.
考点：本题考查的是翻折变换，勾股定理
点评：解答此题的关键是熟练掌握折叠的性质：折叠前后图形的形状和大小不变，对应边和对应角相等．
练习册系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
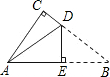如图是一张直角三角形的纸片，两直角边AC=6cm、BC=8cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为（ ）| A、4cm | B、5cm | C、6cm | D、10cm |
如图是一张直角三角形的纸片，两直角边AC=6cm、BC=8cm，现将△ABC折叠，使点B与点A重合，折痕为DE，则BE的长为（ ）
（2012•普陀区一模）如图是一张直角三角形的纸片，直角边AC=6cm，
（2012•香坊区一模）如图是一张直角三角形的纸片．两直角边AC=6cm，BC=8cm将△ABC折叠，使点B与点A重合，折痕为DE，则AD的长为（ ）