题目内容
10. 如图所示,已知CE⊥AB,DF⊥AB,垂足分别为点E、F,且AC=BD,AF=BE.求证:∠C=∠D.
如图所示,已知CE⊥AB,DF⊥AB,垂足分别为点E、F,且AC=BD,AF=BE.求证:∠C=∠D.
分析 根据AF=BE得出AE=BF,再利用直角三角形的全等的判定与性质证明即可.
解答 证明:∵AF=BE,
∴AF-EF=BE-EF,即AE=BF.
∵CE⊥AB,DF⊥AB,
∴∠AEC=∠BFD=90°.
在Rt△AEC和Rt△BFD中,
$\left\{\begin{array}{l}{AE=BF}\\{AC=DB}\end{array}\right.$,
∴Rt△AEC≌Rt△BFD.
∴∠C=∠D.
点评 本题主要考查的是全等三角形的性质和判定、平行线的性质,证得AE=BF,从而得到Rt△AEC≌Rt△BFD是解题的关键.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
20.下列图形中既是中心对称图形又是轴对称图形的是( )
| A. | 等边三角形 | B. | 菱形 | C. | 平行四边形 | D. | 梯形 |
5.加一次暴风雨袭击过后,人们发现一棵9m高的大树被从离地面4m高的地方折断,则树顶与地面的接触点距树根可能是( )
| A. | 1m | B. | 9m | C. | 3m | D. | 13m |
15.下列说法正确的是( )
| A. | 0.720精确到0.001 | B. | 3.6万精确到个位 | ||
| C. | 5.078精确到百分位 | D. | 数字3000是一个近似数 |
20.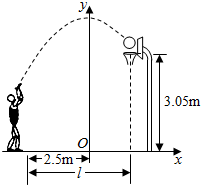 在某次投篮中,球从出手到投中篮圈中心的运动路径是抛物线y=-$\frac{1}{5}$x2+3.5的一部分(如图),则他与篮底的水平距离l(如图)是( )
在某次投篮中,球从出手到投中篮圈中心的运动路径是抛物线y=-$\frac{1}{5}$x2+3.5的一部分(如图),则他与篮底的水平距离l(如图)是( )
 在某次投篮中,球从出手到投中篮圈中心的运动路径是抛物线y=-$\frac{1}{5}$x2+3.5的一部分(如图),则他与篮底的水平距离l(如图)是( )
在某次投篮中,球从出手到投中篮圈中心的运动路径是抛物线y=-$\frac{1}{5}$x2+3.5的一部分(如图),则他与篮底的水平距离l(如图)是( )| A. | 3.5m | B. | 4m | C. | 4.5m | D. | 4.6m |
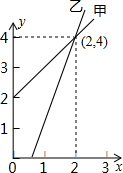 如图是甲、乙两家商店销售A种商品的销售价y(元)与销售量x(件)之间的函数的图象,请根据图象提供的信息,写出4个你认为正确的结论:
如图是甲、乙两家商店销售A种商品的销售价y(元)与销售量x(件)之间的函数的图象,请根据图象提供的信息,写出4个你认为正确的结论: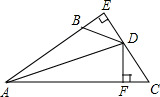 如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AB+AC=2AE中正确的是①②④.
如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AB+AC=2AE中正确的是①②④.