题目内容
11.甲、乙两校分别有一男一女共4名教师报名到农村中学支教.(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是$\frac{1}{2}$.
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率.
分析 (1)根据甲、乙两校分别有一男一女,列出树状图,得出所有情况,再根据概率公式即可得出答案;
(2)根据题意先画出树状图,得出所有情况数,再根据概率公式即可得出答案.
解答 解:(1)根据题意画图如下:
共有4种情况,其中所选的2名教师性别相同的有2种,
则所选的2名教师性别相同的概率是$\frac{2}{4}$=$\frac{1}{2}$;
故答案为:$\frac{1}{2}$;
(2)将甲、乙两校报名的教师分别记为甲1、甲2、乙1、乙2(注:1表示男教师,2表示女教师),树状图如图所示:
所以P(两名教师来自同一所学校)=$\frac{4}{12}$=$\frac{1}{3}$.
点评 本题考查列表法和树状图法,注意结合题意中“写出所有可能的结果”的要求,使用列举法,注意按一定的顺序列举,做到不重不漏.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1.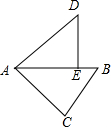 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )
如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )
 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )
如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则B、D两点间的距离为( )| A. | $\sqrt{10}$ | B. | 2$\sqrt{2}$ | C. | 3 | D. | 2$\sqrt{5}$ |
16. 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
 如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )
如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长为( )| A. | $\frac{9}{5}$ | B. | $\frac{12}{5}$ | C. | $\frac{16}{5}$ | D. | $\frac{18}{5}$ |
3. 如图,BD是⊙O的直径,点A、C在⊙O上,$\widehat{AB}$=$\widehat{BC}$,∠AOB=60°,则∠BDC的度数是( )
如图,BD是⊙O的直径,点A、C在⊙O上,$\widehat{AB}$=$\widehat{BC}$,∠AOB=60°,则∠BDC的度数是( )
 如图,BD是⊙O的直径,点A、C在⊙O上,$\widehat{AB}$=$\widehat{BC}$,∠AOB=60°,则∠BDC的度数是( )
如图,BD是⊙O的直径,点A、C在⊙O上,$\widehat{AB}$=$\widehat{BC}$,∠AOB=60°,则∠BDC的度数是( )| A. | 60° | B. | 45° | C. | 35° | D. | 30° |
8.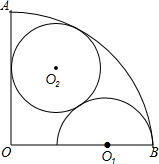 如图,扇形AOB的半径为3,AO⊥BO,O1是半径OB上一圆心,O1B=1,以O1为圆心,O1B为半径在扇形AOB的形内作半圆O1,又⊙O2与半圆O1外切,与AOI、弧AB都相切.求⊙O2的半径.
如图,扇形AOB的半径为3,AO⊥BO,O1是半径OB上一圆心,O1B=1,以O1为圆心,O1B为半径在扇形AOB的形内作半圆O1,又⊙O2与半圆O1外切,与AOI、弧AB都相切.求⊙O2的半径.
 如图,扇形AOB的半径为3,AO⊥BO,O1是半径OB上一圆心,O1B=1,以O1为圆心,O1B为半径在扇形AOB的形内作半圆O1,又⊙O2与半圆O1外切,与AOI、弧AB都相切.求⊙O2的半径.
如图,扇形AOB的半径为3,AO⊥BO,O1是半径OB上一圆心,O1B=1,以O1为圆心,O1B为半径在扇形AOB的形内作半圆O1,又⊙O2与半圆O1外切,与AOI、弧AB都相切.求⊙O2的半径.
9.以下列各线段为边,能组成直角三角形的是( )
| A. | 2,5,8 | B. | 1,1,2 | C. | 4,6,8 | D. | 3,4,5 |
