题目内容
9. 如图是一块△ABC余料,已知AB=20cm,BC=7cm,AC=15cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是( )
如图是一块△ABC余料,已知AB=20cm,BC=7cm,AC=15cm,现将余料裁剪成一个圆形材料,则该圆的最大面积是( )| A. | πcm2 | B. | 2πcm2 | C. | 4πcm2 | D. | 8πcm2 |
分析 当该圆为三角形内切圆时面积最大,设内切圆半径为r,则该三角形面积可表示为:$\frac{1}{2}•r•(AB+BC+AC)$=21r,利用三角形的面积公式可表示为$\frac{1}{2}$•BC•AD,利用勾股定理可得AD,易得三角形ABC的面积,可得r,求得圆的面积.
解答 解:如图1所示,
S△ABC=$\frac{1}{2}$•r•(AB+BC+AC)=$\frac{1}{2}•r•42$=21r,
过点A作AD⊥BC交BC的延长线于点D,如图2,
设CD=x,
由勾股定理得:在Rt△ABD中,
AD2=AB2-BD2=400-(7+x)2,
在Rt△ACD中,AD2=AC2-x2=225-x2,
∴400-(7+x)2=225-x2,
解得:x=9,
∴AD=12,
∴S△ABC=$\frac{1}{2}BC•AD$=$\frac{1}{2}$×7×12=42,
∴21r=42,
∴r=2,
该圆的最大面积为:S=πr2=π•22=4π(cm2),
故选C.
点评 本题主要考查了三角形的内切圆的相关知识及勾股定理的运用,运用三角形内切圆的半径表示三角形的面积是解答此题的关键.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
20.使$\sqrt{x-1}$有意义的x的取值范围是( )
| A. | x≠1 | B. | x≥1 | C. | x>1 | D. | x≥0 |
14.下列事件中,是必然事件的为( )
| A. | 3天内会下雨 | |
| B. | 打开电视机,正在播放广告 | |
| C. | 367人中至少有2人公历生日相同 | |
| D. | 某妇产医院里,下一个出生的婴儿是女孩 |
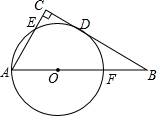 如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.
如图,在△ABC中,∠C=90°,以AB上一点O为圆心,OA长为半径的圆恰好与BC相切于点D,分别交AC、AB于点E、F.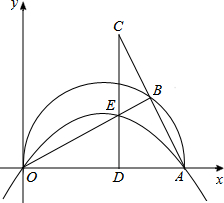 如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆,B为半圆上一点,连接AB并延长至C,使BC=AB,过C作CD⊥x轴于点D,交线段OB于点E,已知CD=8,抛物线经过O、E、A三点.
如图,在平面直角坐标系中,点A(10,0),以OA为直径在第一象限内作半圆,B为半圆上一点,连接AB并延长至C,使BC=AB,过C作CD⊥x轴于点D,交线段OB于点E,已知CD=8,抛物线经过O、E、A三点. 如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若CD=5,则EF的长为5.
如图,在Rt△ABC中,∠ACB=90°,点D,E,F分别为AB,AC,BC的中点.若CD=5,则EF的长为5.