��Ŀ����
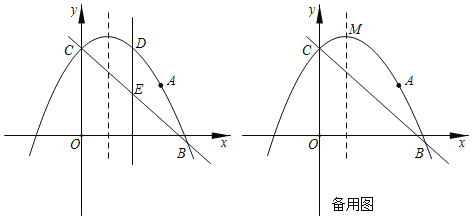
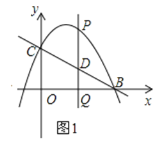
����Ŀ����ͼ1��ֱ��y����![]() x+2��x�ύ�ڵ�B����y�ύ�ڵ�C��������y��-
x+2��x�ύ�ڵ�B����y�ύ�ڵ�C��������y��-![]() x2+bx+c����B��C���㣬��P���������ϵ�һ�����㣬����P��PQ��x�ᣬ����ΪQ����ֱ��y����
x2+bx+c����B��C���㣬��P���������ϵ�һ�����㣬����P��PQ��x�ᣬ����ΪQ����ֱ��y����![]() x+2�ڵ�D�����P�ĺ�����Ϊm��
x+2�ڵ�D�����P�ĺ�����Ϊm��
��1����������ߵĺ�������ʽ��
��2������P��D��O��CΪ������ı�����ƽ���ı��Σ����Q�����ꣻ
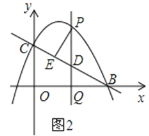
��3����ͼ2������Pλ��ֱ��BC�Ϸ�����������ʱ������P��PE��BC�ڵ�E����PEȡ�����ֵʱ��P�����꣬����PE�����ֵ��
���𰸡���1��y����![]() x2+
x2+![]() x+2����2��(2��0)��(2+2
x+2����2��(2��0)��(2+2![]() ��0)��(2��2
��0)��(2��2![]() ��0)����3��P(2��3)��PE���ֵΪ
��0)����3��P(2��3)��PE���ֵΪ![]() ��
��
��������
��1������ֱ��y����![]() x+2��x�ύ�ڵ�B����y�ύ�ڵ�C�����B��C�������꣬����y��-
x+2��x�ύ�ڵ�B����y�ύ�ڵ�C�����B��C�������꣬����y��-![]() x2+bx+c�ɵù���b��c�Ķ�Ԫһ�η����飬�ⷽ�������b��c��ֵ���ɵô𰸣�
x2+bx+c�ɵù���b��c�Ķ�Ԫһ�η����飬�ⷽ�������b��c��ֵ���ɵô𰸣�
��2������PQ��x�ᣬֱ��y����![]() x+2�ڵ�D����P�ĺ�����Ϊm����m��ʾ��D��Q�������꣬����ƽ���ı��ε����ʿɵ�OC=PD=2�������������빫ʽ���m��ֵ���ɵô𰸣�
x+2�ڵ�D����P�ĺ�����Ϊm����m��ʾ��D��Q�������꣬����ƽ���ı��ε����ʿɵ�OC=PD=2�������������빫ʽ���m��ֵ���ɵô𰸣�
��3�����ù��ɶ��������BC�ij�������ƽ���ߵ����ʿɵá�OCB����PDE����֤����PED�ס�BOC���������������ε����ʿ���m��ʾ��PE�ij������ݶ��κ��������ʼ��ɵô𰸣�
��1����ֱ��y����![]() x+2��x�ύ�ڵ�B����y�ύ�ڵ�C��
x+2��x�ύ�ڵ�B����y�ύ�ڵ�C��
���B��C������ֱ�Ϊ��4��0������0��2����
��������y��-![]() x2+bx+c����B��C���㣬
x2+bx+c����B��C���㣬
��![]() ��
��
���![]() ��
��
����κ�������ʽΪy����![]() x2+
x2+![]() x+2��
x+2��
��2����P�����������ϣ�������Ϊm��
��P��������m����![]() m2+
m2+![]() m+2����
m+2����
��PQ��x�ᣬ����ΪQ����ֱ��y����![]() x+2�ڵ�D��
x+2�ڵ�D��
��Q������m��0����D��������m����![]() m+2����
m+2����
��P��D��O��CΪ������ı���Ϊƽ���ı���ʱ������PD��OC��2��
��|��![]() m2+
m2+![]() m+2������
m+2������![]() m+2��|��2����|��
m+2��|��2����|��![]() m2+2m|��2��
m2+2m|��2��
����![]() m2+2m��2ʱ��
m2+2m��2ʱ��
��ã�m��2��
��Q������2��0����
����![]() m2+2m����2ʱ��
m2+2m����2ʱ��
��ã�m��2��2![]() ��
��
��Q������2+2![]() ��0����2��2
��0����2��2![]() ��0����
��0����
���Ͽ�֪��Q������Ϊ��2��0����2+2![]() ��0����2��2
��0����2��2![]() ��0����
��0����
��3���ɣ�2����֪P������Ϊ��m����![]() m2+
m2+![]() m+2����Q������m��0����D��������m����
m+2����Q������m��0����D��������m����![]() m+2����
m+2����
��PD����![]() m2+2m��
m2+2m��
��Rt��OBC��OC��2��OB��4��
��BC��![]() =2
=2![]() ��
��
��PQ��OC��
���OCB����PDE��
��PE��BC��
���PED����COB��90����
���PED�ס�BOC��
��![]() ��
��
��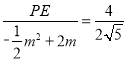 ��
��
���PE��![]() ��
��
��P��ֱ��BC�Ϸ���
��0��m��4��
�൱m��2ʱ PE�����ֵ![]() ��
��
��m��2ʱ����![]() m2+
m2+![]() m+2=3��
m+2=3��
���ʱP������Ϊ��2��3����

 ��������ϵ�д�
��������ϵ�д� ��ӡ�Ļ���ʱ����ϵ�д�
��ӡ�Ļ���ʱ����ϵ�д�