Question

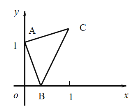
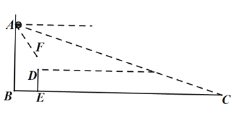
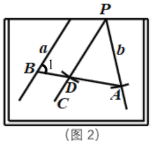
【题目】如图，为等边三角形，为其内心，射线交于点， 点为射线上一动点，将射线绕点逆时针旋转，与射线交于点，当时，的长度为__________

Answer 1

【答案】或；

【解析】

根据等边三角形的性质和内心的定义可得∠BAC=∠ABC=∠ACB=60°，AD平分∠BAC，AB=BC=AC，然后利用锐角三角函数求出BD、CD、OD和OC，然后根据点P和点O的相对位置分类讨论，分别画出对应的图形，利用全等三角形的判定及性质、锐角三角函数和相似三角形的判定及性质即可求出结论．

解：∵为等边三角形，为其内心，

∴∠BAC=∠ABC=∠ACB=60°，AD平分∠BAC，AB=BC=AC

∴AD⊥BC，BD=CD，∠BAD=∠CAD=∠BAC=30°

∴BD=CD==，AB =AC=BC=2BD=

连接OC

易知OC=OA，∠OCD=30°

在Rt△OCD中，OD=CD·tan∠OCD=2，OC=2OD=4

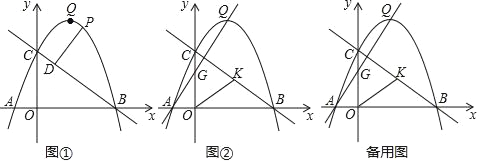
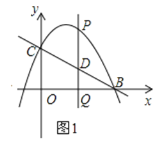
①当点P在点O上方时，如下图所示，设射线绕点逆时针旋转后，点P的对应点为E，连接BE，过点E作EF⊥BC于F

∴∠PCE=60°，EC=PC，AP=AD－OD－PO=3

∴∠PCE=∠ACB=60°

∴∠ECB=∠PCA

∵BC=AC

∴△ECB≌△PCA

∴BE=AP=3，∠EBC=∠PAC=30°

∴EF=BE·sin∠EBC=,BF= BE·cos∠EBC=

∴CF=BC－BF=

∵EF⊥BC，AQ⊥BC

∴EF∥AQ

∴△CDQ∽△CFE

∴

即

解得：DQ=；

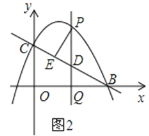
②当点P在点O下方时，如下图所示，设射线绕点逆时针旋转后，点P的对应点为E，连接BE，过点E作EF⊥BC于F

∴∠PCE=60°，EC=PC，AP=AD－OD＋PO=5

∴∠PCE=∠ACB=60°

∴∠ECB=∠PCA

∵BC=AC

∴△ECB≌△PCA

∴BE=AP=5，∠EBC=∠PAC=30°

∴EF=BE·sin∠EBC=,BF= BE·cos∠EBC=

∴CF=BC－BF=

∵EF⊥BC，AQ⊥BC

∴EF∥AQ

∴△CDQ∽△CFE

∴

即

解得：DQ=；

综上：DQ=或

故答案为：或．