题目内容
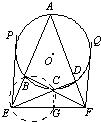7、如图，ABCD是⊙O的内接四边形，延长AB和DC相交于E，延长AB和DC相交于E，延长AD和BC相交于F，EP和FQ分别切⊙O于P、Q．求证：EP2+FQ2=EF2．分析：因EP和FQ是⊙O的切线，由结论联想到切割线定理，构造辅助圆使EP、FQ向EF转化．
解答：证明：如图，作△BCE的外接圆交EF于G，连接CG，
因∠FDC=∠ABC=∠CGE，故F、D、C、G四点共圆，
由切割线定理，有EF2=（EG+GF）•EF，
=EG•EF+GF•EF，
=EC•ED+FC•FB，
=EC•ED+FC•FB，
=EP2+FQ2，
即EP2+FQ2=EF2．
证明：如图，作△BCE的外接圆交EF于G，连接CG，因∠FDC=∠ABC=∠CGE，故F、D、C、G四点共圆，
由切割线定理，有EF2=（EG+GF）•EF，
=EG•EF+GF•EF，
=EC•ED+FC•FB，
=EC•ED+FC•FB，
=EP2+FQ2，
即EP2+FQ2=EF2．
点评：本题考查了切割线定理和四点共圆问题，这是综合题有一定的难度．
练习册系列答案
名师导航单元期末冲刺100分系列答案
名校名卷单元同步训练测试题系列答案
相关题目
如图四边形ABCD是⊙O的内接四边形，AB是⊙O的直径，若再增加一个条件，就可使四边形ABCD成为等腰梯形，你所增加的条件是（只写出一个条件，图中不再增加其他的字母和线段．（给出证明）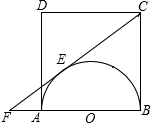
如图，ABCD是边长为2 a的正方形，AB为半圆O的直径，CE切⊙O于E，与BA的延长线交于F，求EF的长．
如图，ABCD是边长为1的正方形，EFGH是内接于ABCD的正方形，AE=a，AF=b，若SEFGH=| 2 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，ABCD是正方形，G是BC上的一点，DE⊥AG于E，BF⊥AG于F．