题目内容
20.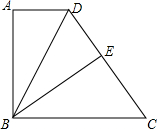 如图,在四边形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E.
如图,在四边形ABCD中,AD∥BC,AB⊥AD,BC=CD,BE⊥CD,垂足为E.(1)求证:DA=DE;
(2)若AD=4,BC=10,求AB.
分析 (1)利用已知条件证明△ABD≌△EBD,根据确定三角形的对应边相等得到DA=DE;
(2)由△ABD≌△EBD,得到AD=DE=4,从而求得CE=6,在Rt△BCE中,利用勾股定理求得BE2=BC2-CE2=8,即可解答.
解答 解:(1)∵AB⊥AD,BE⊥DC
∴∠A=∠BED=90°,
∵BC=CD
∴∠DBC=∠BDC,
∵AD∥BC
∴∠DBC=∠ADB,
∴∠BDC=∠ADB,
在△ABD和△EBD中,
$\left\{\begin{array}{l}{∠A=∠BED}\\{∠ADB=∠EDB}\\{BD=BD}\end{array}\right.$,
∴△ABD≌△EBD,
∴DA=DE.
(2)∵△ABD≌△EBD,
∴AD=DE=4,
∵BC=CD=10,
∴CE=6,
在Rt△BCE中,
BE2=BC2-CE2=8,
∴AB=BE=8.
点评 本题考查了全等三角形的性质与判定,解决本题的关键是证明△ABD≌△EBD.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
11.股民小明上周末买进某公司股票1000股,每股23元,如表为本周内每日该股票的涨跌情况(单位:元)
(1)星期三收盘时,每股是多少元?
(2)本周内最高价是每股多少元?最低价是每股多少元?
(3)已知小明买进股票时付了0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,如果小明在周末收盘前将全部股票卖出,他的收益情况如何?
| 星期 | 一 | 二 | 三 | 四 | 五 |
| 每股涨跌 | +2 | +4.5 | -1 | -2.5 | -2 |
(2)本周内最高价是每股多少元?最低价是每股多少元?
(3)已知小明买进股票时付了0.15%的手续费,卖出时需付成交额0.15%的手续费和0.1%的交易税,如果小明在周末收盘前将全部股票卖出,他的收益情况如何?
12.下列说法:(1)全等三角形的对应边相等;(2)全等三角形的对应角相等;(3)全等三角形的周长相等;(4)周长相等的两个三角形相等;(5)全等三角形的面积相等;(6)面积相等的两个三角形全等.其中不正确的是( )
| A. | (4)(5) | B. | (4)(6) | C. | (3)(6) | D. | (3)(4)(5)(6) |
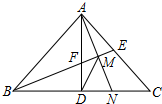 如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,AM的延长线交BC于点N,连接DM,下列结论:①DF=DN; ②△DMN为等腰三角形;③DM平分∠BMN;④AE=$\frac{2}{3}$EC;
如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于点D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,AM的延长线交BC于点N,连接DM,下列结论:①DF=DN; ②△DMN为等腰三角形;③DM平分∠BMN;④AE=$\frac{2}{3}$EC;