题目内容
如图，在⊙O中，弦AC与BD交于点E，AB=8，AE=6，ED=4，求CD的长．考点：圆周角定理,相似三角形的判定与性质
专题：计算题
分析：根据圆周角定义得到∠B=∠C，∠A=∠D，则可判断△ABE∽△CDE，然后根据相似比计算CD的长．
解答：解：∵∠B=∠C，∠A=∠D，
∴△ABE∽△CDE，
∴
=
，即
=
，
∴CD=
．
∴△ABE∽△CDE，
∴
| AB |
| CD |
| AE |
| DE |
| 8 |
| CD |
| 6 |
| 4 |
∴CD=
| 16 |
| 3 |
点评：本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．也考查了相似三角形的判定与性质．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，P为⊙O的直径AB的延长线上一点，PC切⊙O于点C，若∠P=26°，则∠A等于（ ）| A、32° | B、36° |
| C、38° | D、42° |
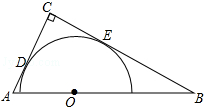如图，Rt△ABC中，∠ACB=90°，AC=4，BC=6，以斜边AB上的一点O为圆心所作的半圆分别与AC、BC相切于点D、E，则AD为（ ）| A、1 | B、1.5 |
| C、1.6 | D、2.5 |
如图，△ABC的三个顶点都在格点上，A点的坐标为（-4，2），B点的坐标为（-2，1），C点的坐标为（-1，3）两等边三角形的边长之比为1：3，那么它们的面积之比是（ ）
| A、1：9 | ||
B、1：
| ||
| C、1：3 | ||
| D、无法确定 |
点P（4，-3）关于原点的对称点是（ ）
| A、（4，3） |
| B、（-3，4） |
| C、（-4，3） |
| D、（3，-4） |