题目内容
在半径为10cm的圆中截取两个半径分别为acm和bcm的圆,且a+b=10,若所剩的阴影部分的面积为y,则y与a的关系式为 ,当a= 时,y有最大值 cm2.
考点:根据实际问题列二次函数关系式
专题:
分析:首先表示出两圆的半径进而得出其面积,即可得出答案.
解答:解:∵半径为10cm的圆中截取两个半径分别为acm和bcm的圆,且a+b=10,
∴b=10-a,
∵所剩的阴影部分的面积为y,
则y与a的关系式为:y=π×102-πa2-π(10-a)2=-πa2+20πa,
当a=-
=10时,y最大为:
=100π.
故答案为:y=-πa2+20πa,100π.
∴b=10-a,
∵所剩的阴影部分的面积为y,
则y与a的关系式为:y=π×102-πa2-π(10-a)2=-πa2+20πa,
当a=-
| 20π |
| 2×(-π) |
| -(20π)2 |
| 4×(-π) |
故答案为:y=-πa2+20πa,100π.
点评:此题主要考查了二次函数最值求法以及圆的面积求法等知识,得出y与a的关系式是解题关键.

练习册系列答案
相关题目
 如图,已知DE⊥AC于点E,BC⊥AC于点C,FG⊥AB于点G,∠1=∠2,求证:CD⊥AB.
如图,已知DE⊥AC于点E,BC⊥AC于点C,FG⊥AB于点G,∠1=∠2,求证:CD⊥AB. 如图,△ABC∽△DBA,∠BAC=∠ADB,写出其余的对应角和对应边的比例式.
如图,△ABC∽△DBA,∠BAC=∠ADB,写出其余的对应角和对应边的比例式. 如图,AB∥CD,设α=∠1+∠2+∠3,β=∠4+∠5,则α与β之间有怎样的数量关系?写出你的猜测和理由.
如图,AB∥CD,设α=∠1+∠2+∠3,β=∠4+∠5,则α与β之间有怎样的数量关系?写出你的猜测和理由.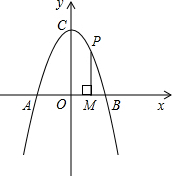 如图,抛物线y=ax2+4经过x轴上的一点A(-2,0),抛物顶点为点C,P是抛物线上的一动点.过P(不与B重合)作x轴垂线,垂足为点M,如图,若△AMC为等腰三角形,求P点的坐标.
如图,抛物线y=ax2+4经过x轴上的一点A(-2,0),抛物顶点为点C,P是抛物线上的一动点.过P(不与B重合)作x轴垂线,垂足为点M,如图,若△AMC为等腰三角形,求P点的坐标. 从下面的两个立体图形中任选其一,画出它的三种视图.
从下面的两个立体图形中任选其一,画出它的三种视图.