Question

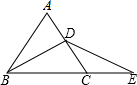已知，如图，在等边三角形ABC的AC边上取中点D，BC的延长线上取一点E，使CE=CD．
（1）求证：BD=DE；
（2）若等边三角形的边长为4，试求△DCE的面积．

Answer 1

考点：等边三角形的性质,等腰三角形的性质

专题：

分析：（1）欲证BD=DE，只需证∠DBE=∠E，根据等边三角形的性质及角的等量关系可证明∠DBE=∠E=30°．
（2）作DM⊥BE于M，根据等边三角形的性质求得BD=

3

2

BC=2

3

，进而求得DM=

3

，BE=6，根据三角形面积公式即可求得．

解答：证明：（1）∵△ABC为等边三角形，BD是AC边的中线，
∴BD⊥AC，BD平分∠ABC，∠DBE=

1

2

∠ABC=30°．
∵CD=CE，
∴∠CDE=∠E．
∵∠ACB=60°，且∠ACB为△CDE的外角，
∴∠CDE+∠E=60°．
∴∠CDE=∠E=30°，
∴∠DBE=∠DEB=30°，
∴BD=DE．
（2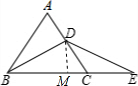）作DM⊥BE于M，
∵等边三角形的边长为4，
∴BD=

3

2

BC=2

3

，
∵∠DBE=∠DEB=30°，
∴DM=

3

，BM=

3

2

BD=3，
∴BE=2BM=6，
∴△DCE的面积=

1

2

BE•DM=

1

2

×6×

3

=3

3

．

点评：本题考查等腰三角形与等边三角形的性质及三角形内角和为180°等知识．此类已知三角形边之间的关系求角的度数的题，一般是利用等腰（等边）三角形的性质得出有关角的度数，进而求出所求角的度数．