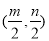题目内容
(本题满分12分)在平面直角坐标系中,抛物线y=x2+(k﹣1)x﹣k与直线y=kx+1交于A,B两点,点A在点B的左侧.

(1)如图1,当k=1时,直接写出A,B两点的坐标;
(2)在(1)的条件下,点P为抛物线上的一个动点,且在直线AB下方,试求出△ABP面积的最大值及此时点P的坐标;
(3)如图2,抛物线y=x2+(k﹣1)x﹣k(k>0)与x轴交于点C、D两点(点C在点D的左侧),在直线y=kx+1上是否存在唯一一点Q,使得∠OQC=90°?若存在,请求出此时k的值;若不存在,请说明理由.
(1)A(﹣1,0),B(2,3);(2)△ABP面积最大值为 ,此时点P坐标为(
,此时点P坐标为( ,﹣
,﹣ );(3)
);(3)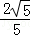 或1.
或1.
【解析】
试题分析:(1)当k=1时,联立抛物线与直线的解析式,解方程求得点A、B的坐标;
(2)如答图2,作辅助线,求出△ABP面积的表达式,然后利用二次函数的性质求出最大值及点P的坐标;
(3)“存在唯一一点Q,使得∠OQC=90°”的含义是,以OC为直径的圆与直线AB相切于点Q,由圆周角定理可证,此时∠OQC=90°且点Q为唯一.以此为基础,构造相似三角形,利用比例式列出方程,求得k的值,注意另外注意一点是考虑直线AB是否与抛物线交于C点,此时亦存在唯一一点Q,使得∠OQC=90°.
试题解析:解:(1)当k=1时,抛物线解析式为y=x2﹣1,直线解析式为y=x+1.
联立两个解析式,得:x2﹣1=x+1,
解得:x=﹣1或x=2,
当x=﹣1时,y=x+1=0;当x=2时,y=x+1=3,
∴A(﹣1,0),B(2,3).
(2)设P(x,x2﹣1).
如答图2所示,过点P作PF∥y轴,交直线AB于点F,则F(x,x+1).
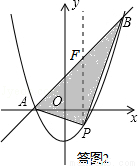
∴PF=yF﹣yP=(x+1)﹣(x2﹣1)=﹣x2+x+2.
S△ABP=S△PFA+S△PFB= ,
,
∴S△ABP= (﹣x2+x+2)=﹣
(﹣x2+x+2)=﹣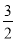 (x﹣
(x﹣ )2+
)2+
当x= 时,yP=x2﹣1=﹣
时,yP=x2﹣1=﹣ .
.
∴△ABP面积最大值为 ,此时点P坐标为(
,此时点P坐标为( ,﹣
,﹣ ).
).
(3)设直线AB:y=kx+1与x轴、y轴分别交于点E、F,
则E(﹣ ,0),F(0,1),OE=
,0),F(0,1),OE= ,OF=1.
,OF=1.
在Rt△EOF中,由勾股定理得:EF= =
= .
.
令y=x2+(k﹣1)x﹣k=0,即(x+k)(x﹣1)=0,解得:x=﹣k或x=1.
∴C(﹣k,0),OC=k.
Ⅰ、假设存在唯一一点Q,使得∠OQC=90°,如答图3所示,
则以OC为直径的圆与直线AB相切于点Q,根据圆周角定理,此时∠OQC=90°.

设点N为OC中点,连接NQ,则NQ⊥EF,NQ=CN=ON=.
∴EN=OE﹣ON=﹣.
∵∠NEQ=∠FEO,∠EQN=∠EOF=90°,
∴△EQN∽△EOF,
∴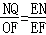 ,即:
,即: ,
,
解得:k=±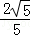 ,
,
∵k>0,
∴k=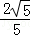 .
.
∴存在唯一一点Q,使得∠OQC=90°,此时k=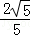 .
.
Ⅱ、若直线AB过点C时,此时直线与圆的交点只有另一点Q点,故亦存在唯一一点Q,使得∠OQC=90°,
将C(﹣k,0)代入y=kx+1中,可得k=1,k=-1(舍去),
故亦存在唯一一点Q,使得∠OQC=90°,此时k=1.
综上所述,k=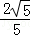 或1时,存在唯一一点Q,使得∠OQC=90°.
或1时,存在唯一一点Q,使得∠OQC=90°.
考点:二次函数综合题;一次函数的图象与性质;直线与圆的位置关系.
考点分析: 考点1:二次函数 定义:一般地,如果
 (a,b,c是常数,a≠0),那么y叫做x 的二次函数。
(a,b,c是常数,a≠0),那么y叫做x 的二次函数。 ①所谓二次函数就是说自变量最高次数是2;
②二次函数
 (a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时,
(a≠0)中x、y是变量,a,b,c是常数,自变量x 的取值范围是全体实数,b和c可以是任意实数,a是不等于0的实数,因为a=0时, 变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。
变为y=bx+c若b≠0,则y=bx+c是一次函数,若b=0,则y=c是一个常数函数。③二次函数
 (a≠0)与一元二次方程
(a≠0)与一元二次方程 (a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式:
(a≠0)有密切联系,如果将变量y换成一个常数,那么这个二次函数就是一个一元二次函数。
二次函数的解析式有三种形式: (1)一般式:
 (a,b,c是常数,a≠0);
(a,b,c是常数,a≠0); (2)顶点式:
 (a,h,k是常数,a≠0)
(a,h,k是常数,a≠0) (3)当抛物线
 与x轴有交点时,即对应二次好方程
与x轴有交点时,即对应二次好方程 有实根x1和x2存在时,根据二次三项式的分解因式
有实根x1和x2存在时,根据二次三项式的分解因式 ,二次函数
,二次函数 可转化为两根式
可转化为两根式 。如果没有交点,则不能这样表示。
。如果没有交点,则不能这样表示。 二次函数的一般形式的结构特征:
①函数的关系式是整式;
②自变量的最高次数是2;
③二次项系数不等于零。 二次函数的判定:
二次函数的一般形式中等号右边是关于自变量x的二次三项式;
当b=0,c=0时,y=ax2是特殊的二次函数;
判断一个函数是不是二次函数,在关系式是整式的前提下,如果把关系式化简整理(去括号、合并同类项)后,能写成
 (a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
(a≠0)的形式,那么这个函数就是二次函数,否则就不是。
试题属性
- 题型:
- 难度:
- 考核:
- 年级:

 名校课堂系列答案
名校课堂系列答案
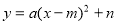 的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为
的顶点在线段AB上运动,与x轴交于C、D两点(C在D的左侧),点C的横坐标最小值为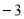 ,则点D的横坐标最大值为_______。
,则点D的横坐标最大值为_______。
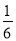 B.
B.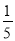 C.
C.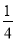 D.
D.
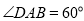 ,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.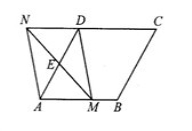
 中,
中, 、
、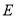 分别是边
分别是边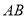 、
、 的中点,
的中点, .现将
.现将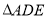 沿
沿 折叠,点
折叠,点 落在三角形所在平面内的点为
落在三角形所在平面内的点为 ,则
,则 的度数为 °.
的度数为 °.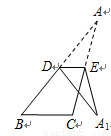
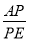 的值;
的值;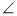 BAE=
BAE=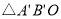 ,其中A、B的对应点分别为
,其中A、B的对应点分别为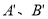 ,
,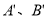 均在图中格点上,若线段AB上有一点
均在图中格点上,若线段AB上有一点 ,则点
,则点 在
在 上的对应点
上的对应点 的坐标为( ).
的坐标为( ).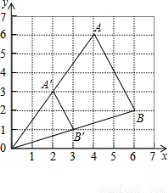
 B、
B、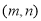 C、
C、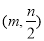 D、
D、