题目内容
13.已知a+$\frac{1}{a}$=$\sqrt{5}$(a>1),求:(1)a-$\frac{1}{a}$的值;
(2)$\frac{{a}^{2}}{{a}^{4}{+a}^{2}+1}$的值.
分析 (1)利用完全平方公式可以求解.
(2)利用倒数法解决.
解答 解:(1)∵a+$\frac{1}{a}$=$\sqrt{5}$,
∴(a+$\frac{1}{a}$)2=($\sqrt{5}$)2,
∴a2+2+$\frac{1}{{a}^{2}}$=5,
∴a2+$\frac{1}{{a}^{2}}$=3,
∴a2-2+$\frac{1}{{a}^{2}}$=1,
∴(a-$\frac{1}{a}$)2=1,
∴a-$\frac{1}{a}$=±1,
∵a>1,
∴a-$\frac{1}{a}$=1.
(2)∵a2+$\frac{1}{{a}^{2}}$=3,
∴$\frac{{a}^{4}+{a}^{2}+1}{{a}^{2}}$=a2+1+$\frac{1}{{a}^{2}}$=4,
∴$\frac{{a}^{2}}{{a}^{4}+{a}^{2}+1}$=$\frac{1}{4}$.
点评 本题考查完全平方公式、倒数法,熟练运用公式是解决问题的关键.

练习册系列答案
相关题目
3.某批乒乓球的质量检验结果如下:
(1)a=0.94,b=0.945;
(2)在图中画出这批乒乓球“优等品”频率的折线统计图;
(3)这批乒乓球“优等品”的概率的估计值是0.95.

| 抽取的乒乓球数n | 50 | 100 | 200 | 500 | 1000 | 1500 | 2000 |
| 优等品频数m | 47 | 95 | 189 | 478 | 948 | 1426 | 1898 |
| 优等品频率$\frac{m}{n}$ | a | 0.95 | b | 0.956 | 0.948 | 0.951 | 0.949 |
(2)在图中画出这批乒乓球“优等品”频率的折线统计图;
(3)这批乒乓球“优等品”的概率的估计值是0.95.

8.沿圆锥的母线剪开展平得到的侧面展开图是( )
| A. | 三角形 | B. | 长方形 | C. | 圆 | D. | 扇形 |
 如图,在矩形ABCD中,AB=5cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,且△ABF的面积是30cm2.求AD、CE的长.
如图,在矩形ABCD中,AB=5cm,在边CD上适当选定一点E,沿直线AE把△ADE折叠,使点D恰好落在边BC上一点F处,且△ABF的面积是30cm2.求AD、CE的长.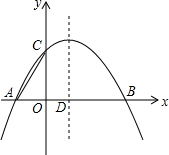 已知二次函数y=ax2+bx+c的图象经过A(-2,0)、B(4,0)、C(O,3)三点,连接AC,该二次函数图象的对称轴与x轴相交于点D.
已知二次函数y=ax2+bx+c的图象经过A(-2,0)、B(4,0)、C(O,3)三点,连接AC,该二次函数图象的对称轴与x轴相交于点D.