题目内容
以下列各数为边长,不能组成直角三角形的是( )
| A、3,4,5 |
| B、5,12,13 |
| C、6,8,10 |
| D、4,5,6 |
考点:勾股定理的逆定理
专题:
分析:根据勾股定理的逆定理知,当三角形中三边存在:a2+b2=c2关系时是直角三角形.
解答:解:A、能,因为32+42=52;
B、能,因为52+122=132;
C、能,因为62+82=102;
D、不能,因为42+52=≠62,不符合勾股定理的逆定理.
故选D.
B、能,因为52+122=132;
C、能,因为62+82=102;
D、不能,因为42+52=≠62,不符合勾股定理的逆定理.
故选D.
点评:本题考查了用勾股定理的逆定理判定直角三角形,即如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形就是直角三角形.

练习册系列答案
相关题目
直线y=2x-6与两坐标轴所围成的三角形面积等于( )
| A、18 | B、6 | C、12 | D、9 |
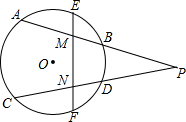 如图,已知圆O的弦AB、CD的延长线相交于点P,连接弧AB、弧CD的中点E、F分别交AB、CD于点M、N,求证:△PNM是等腰三角形.
如图,已知圆O的弦AB、CD的延长线相交于点P,连接弧AB、弧CD的中点E、F分别交AB、CD于点M、N,求证:△PNM是等腰三角形.