Question

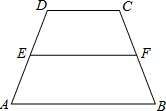
已知如图：在梯形ABCD中，AB∥DC，点E、F分别是两腰AD、BC的中点． 
证明：（1）EF∥AB∥DC；
（2）EF=

1

2

（AB+DC）．

Answer 1

分析：连接AF并延长交BC于点G，则△ADF≌△GCF，可以证得EF是△ABG的中位线，利用三角形的中位线定理即可证得．

解答：解：连接AF并延长交BC于点G．
∵AD∥BC
∴∠DAF=∠G，
在△ADF和△GCF中，

∠DAF=∠G ∠DFA=∠CFG DF=FC

∴△ADF≌△GCF，
∴AF=FG，AD=CG．
又∵AE=EB，
∴EF∥BG，EF=

1

2

BG，
即EF∥AD∥BC，EF=

1

2

（AD+BC）．

点评：本题证明了梯形的中位线定理，通过辅助线转化成三角形的中位线的问题，体现了数学中的转化思想．