题目内容
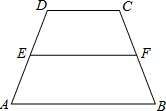
已知如图，在梯形ABCD中，AD∥BC，AB=DC=AD=2，BC=4，求∠B的度数及AC的长。
解：如图，分别作AF⊥BC，DG⊥BC，F、G是垂足，
∴∠AFB=∠DGC=90°。
∵AD∥BC，
∴四边形AFCD是矩形，
∴AF=DG，
∵AB=DC，
∴Rt △AFB≌Rt △DGC，
∴BF=CG，
∵AD=2，BC=4，
∴BF=1，
在Rt△AFB中，
∵cosB=
=
，
∴∠B=60°，
∵BF=1，
∵FC=3，
由勾股定理，得
∴∠B=60°
。
∴∠AFB=∠DGC=90°。
∵AD∥BC，
∴四边形AFCD是矩形，
∴AF=DG，
∵AB=DC，
∴Rt △AFB≌Rt △DGC，
∴BF=CG，
∵AD=2，BC=4，
∴BF=1，
在Rt△AFB中，
∵cosB=
=， ∴∠B=60°，
∵BF=1，
∵FC=3，
由勾股定理，得
∴∠B=60°
。
练习册系列答案
53随堂测系列答案
相关题目
已知如图：在梯形ABCD中，AB∥DC，点E、F分别是两腰AD、BC的中点． 
已知如图：在梯形ABCD中，AB∥DC，点E、F分别是两腰AD、BC的中点． 
（AB+DC）．
