题目内容
已知如图:在梯形ABCD中,AB∥DC,点E、F分别是两腰AD、BC的中点.
证明:(1)EF∥AB∥DC;
(2)EF=
(AB+DC).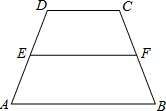
证明:(1)EF∥AB∥DC;
(2)EF=
| 1 |
| 2 |


连接AF并延长交BC于点G.
∵AD∥BC
∴∠DAF=∠G,
在△ADF和△GCF中,
|
∴△ADF≌△GCF,
∴AF=FG,AD=CG.
又∵AE=EB,
∴EF∥BG,EF=
| 1 |
| 2 |
即EF∥AD∥BC,EF=
| 1 |
| 2 |

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 已知如图:在梯形ABCD中,AB∥DC,点E、F分别是两腰AD、BC的中点.
已知如图:在梯形ABCD中,AB∥DC,点E、F分别是两腰AD、BC的中点.  已知如图:在梯形ABCD中,AB∥DC,点E、F分别是两腰AD、BC的中点.
已知如图:在梯形ABCD中,AB∥DC,点E、F分别是两腰AD、BC的中点.  (AB+DC).
(AB+DC).
