题目内容
19.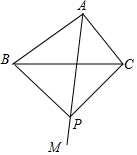 如图,在△ABC中,∠BAC=90°,射线AM平分∠BAC,AB=8,cos∠ACB=$\frac{3}{5}$,点P为射线AM上一点,且PB=PC,则四边形ABPC的面积为49.
如图,在△ABC中,∠BAC=90°,射线AM平分∠BAC,AB=8,cos∠ACB=$\frac{3}{5}$,点P为射线AM上一点,且PB=PC,则四边形ABPC的面积为49.
分析 设AC=3k,BC=5k,根据勾股定理得到AB=4k,得到BC=10,AC=6,过P作PE⊥AB于E,PF⊥于F,求得四边形AEPF是矩形,证得矩形AEPF是正方形,根据全等三角形的性质得到BE=CF,于是得到结论.
解答 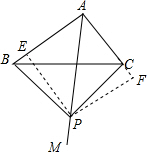 解:∵在△ABC中,∠BAC=90°,AB=8,cos∠ACB=$\frac{3}{5}$,
解:∵在△ABC中,∠BAC=90°,AB=8,cos∠ACB=$\frac{3}{5}$,
∴设AC=3k,BC=5k,
∴AB=4k,
∴k=2,
∴BC=10,AC=6,
过P作PE⊥AB于E,PF⊥于F,
∴四边形AEPF是矩形,
∵射线AM平分∠BAC,
∴PE=PF,
∴矩形AEPF是正方形,
在Rt△PBE与Rt△PFC中$\left\{\begin{array}{l}{PB=PC}\\{PE=PF}\end{array}\right.$,
∴Rt△PBE≌Rt△PFC,
∴BE=CF,
∴AE=AF=7,
∴四边形ABPC的面积=正方形AEPF的面积=7×7=49,
故答案为:49.
点评 本题考查了全等三角形的判定和性质,正方形的判定,角平分线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
相关题目
9.已知x+y=$\sqrt{2}$,|x|+|y|=5$\sqrt{2}$,则x-y的值为( )
| A. | $±2\sqrt{2}$ | B. | $±3\sqrt{2}$ | C. | $±4\sqrt{2}$ | D. | $±5\sqrt{2}$ |
10.式子$-\sqrt{a{x^3}}$(a>0)化简的结果是( )
| A. | $x\sqrt{-ax}$ | B. | $-x\sqrt{-ax}$ | C. | $x\sqrt{ax}$ | D. | $-x\sqrt{ax}$ |
7.某企业对其生产的产品进行抽检,抽检结果如下表:
若该企业生产该产品10000件,估计不合格产品的件数为( )
| 抽检件数 | 10 | 40 | 100 | 200 | 300 | 500 |
| 不合格件数 | 0 | 1 | 2 | 3 | 6 | 10 |
| A. | 80件 | B. | 100件 | C. | 150件 | D. | 200件 |
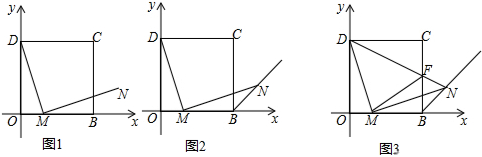
 直线y=$\frac{3}{2}$x与双曲线y=$\frac{k}{x}$的交点A的横坐标为2
直线y=$\frac{3}{2}$x与双曲线y=$\frac{k}{x}$的交点A的横坐标为2