Question

14．如图，把一张矩形纸片ABCD折叠成一个四边形AECD，已知CD=3，折痕CE长为2，则四边形AECD的面积为3$\sqrt{2}$-1．．

Answer 1

分析 记点B的对应点为B′，根据题意可证明BCB′E为正方形，故此可求得BC=BE=$\sqrt{2}$，最后依据梯形的面积公式求解即可．

解答 解：如图所示：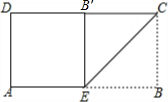

由翻折的性质可知：∠B=∠CB′E=90°，B′C=BC．
∵∠B=∠BCB′=∠CB′B=90°，
∴四边形BCB′E为矩形．
又∵BC=CB′，
∴四边形BCB′E为正方形．
∴BE=BC=$\frac{\sqrt{2}}{2}EC$=$\sqrt{2}$．
∴四边形AECD的面积=$\frac{1}{2}×$（AE+DC）×CB=$\frac{1}{2}×\sqrt{2}×$（6-$\sqrt{2}$）=3$\sqrt{2}$-1．
故答案为：3$\sqrt{2}$-1．

点评 本题主要考查的是翻折的性质、正方形的性质和判定、梯形的面积公式，证得四边形BCB′E为正方形是解题的关键．