题目内容
16. 已知:如图,在?ABCD中,点E、F在BD上,且∠AEB=∠CFD.
已知:如图,在?ABCD中,点E、F在BD上,且∠AEB=∠CFD.(1)求证:四边形AECF是平行四边形;
(2)当四边形AECF是菱形时,四边形ABCD应满足什么条件?(不需要说明理由)
分析 (1)由平行四边形的性质得出AB=CD,∠BAE=∠CDF,由AAS证明证得△ABE≌△CDF,继而证得结论;
(2)由菱形的判定定理容易得出结论.
解答 (1)证明:连接AC交BD于O,如图所示: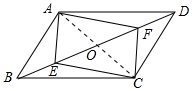
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD.OA=OC,OB=OD,
∴∠ABE=∠CDF.
在△ABE和△CDF中,$\left\{\begin{array}{l}{∠AEB=∠CFD}&{\;}\\{∠BAE=∠DCF}&{\;}\\{AB=CD}&{\;}\end{array}\right.$,
∴△ABE≌△CDF(AAS).
∴BE=DF,
∴OE=OF,
∵OA=OC,
∴四边形AECF是平行四边形;
(2)解:当四边形AECF是菱形时,四边形ABCD应满足AC⊥BD;理由如下:
由(1)得:四边形AECF是平行四边形,
∵AC⊥BD,
∴四边形AECF是菱形.
点评 此题考查了平行四边形的性质、全等三角形的判定与性质以及菱形的判定.此题难度不大,证明四边形是平行四边形是解决问题的关键,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
7.下列图形是中心对称图形.( )
| A. |  | B. |  | C. |  | D. |  |
11.下列事件中,为必然事件的是( )
| A. | 购买一张彩票,中奖 | |
| B. | 打开电视,正在播放广告 | |
| C. | 抛掷一枚硬币,正面向上 | |
| D. | 一个袋中只装有2个黑球,从中摸出一个球是黑球 |
 如图,△ABC中,∠ABC=90°,AB=12,BC=5,AC=13,BD⊥AC于D,则BD=$\frac{60}{13}$.
如图,△ABC中,∠ABC=90°,AB=12,BC=5,AC=13,BD⊥AC于D,则BD=$\frac{60}{13}$.