题目内容
6.已知点A,B的坐标分别为(-4,0)和(2,0),在直线y=-$\frac{1}{2}$x+2上取一点C,若△ABC是直角三角形,则满足条件的点C有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据∠A为直角,∠B为直角与∠C为直角三种情况进行分析.
解答 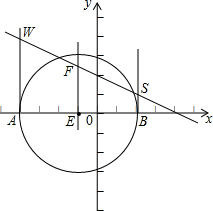 解:由题意知,直线y=-$\frac{1}{2}$x+2与x轴的交点为(4,0),与y轴的交点为(0,2),如图:
解:由题意知,直线y=-$\frac{1}{2}$x+2与x轴的交点为(4,0),与y轴的交点为(0,2),如图:
当∠A为直角时,过点A作x轴的垂线与直线的交点W(-4,4),
当∠B为直角时,过点B作x轴的垂线与直线的交点S(2,1),
当∠C为直角时,过AB中点E(-1,0),作x轴的垂线与直线的交点为F(-1,2.5),则EF=2.5<3,
所以以3为半径,以点E为圆心的圆与直线必有两个交点,
综上所述,共有四个点能与点A,点B组成直角三角形.
故选D.
点评 本题考查的是一次函数图象上点的坐标特征,直角三角形的性质,在解答此题时要分三种情况进行讨论,不要漏解.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
16. 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
 如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )
如图,在平行四边形ABCD中,点E是边AD的中点,EC交对角线BD于点F,则EF:FC等于( )| A. | 3:2 | B. | 3:1 | C. | 1:1 | D. | 1:2 |
17.下列运算正确的是( )
| A. | a2+a3=a5 | B. | a6÷a2=a3 | C. | (-a2)3=a6 | D. | -2a•a2=-2a3 |
1.化简a2•a的结果是( )
| A. | a2 | B. | 2a2 | C. | a3 | D. | a |
18.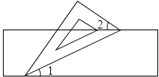 如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=23°,则∠2的度数是( )
如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=23°,则∠2的度数是( )
 如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=23°,则∠2的度数是( )
如图,小聪把一块含有60°角的直角三角板的两个顶点放在直尺的对边上,并测得∠1=23°,则∠2的度数是( )| A. | 23° | B. | 27° | C. | 30° | D. | 37° |
 如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使∠ABC不是直角三角形的概率是$\frac{3}{7}$.
如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使∠ABC不是直角三角形的概率是$\frac{3}{7}$.