题目内容
10.若x2+y2-4x+2y+5=0,求($\frac{x}{2}}$)2010+y2010的值.分析 根据x2+y2-4x+2y+5=0,可以求得x、y的值,从而可以求得所求式子的值.
解答 解:∵x2+y2-4x+2y+5=0,
∴x2-4x+4+y2+2y+1=0,
∴(x-2)2+(y+1)2=0,
∴x-2=0,y+1=0,
解得,x=2,y=-1,
∴($\frac{x}{2}}$)2010+y2010
=$(\frac{2}{2})^{2010}+(-1)^{2010}$
=1+1
=2.
点评 本题考查配方法的应用、非负数的性质,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.下列分式为最简分式的是( )
| A. | $\frac{3b}{15a}$ | B. | $\frac{{a}^{2}-{b}^{2}}{a-b}$ | C. | $\frac{{x}^{2}}{3x}$ | D. | $\frac{{x}^{2}+y2}{x+y}$ |
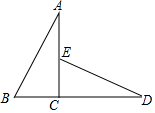 如图,△ABC≌△DEC且∠AED=120°,B,C,D三点在一条直线上,CD=2$\sqrt{3}$cm,AB=4cm,则∠D=30°;AE=(2$\sqrt{3}$-2)cm.
如图,△ABC≌△DEC且∠AED=120°,B,C,D三点在一条直线上,CD=2$\sqrt{3}$cm,AB=4cm,则∠D=30°;AE=(2$\sqrt{3}$-2)cm.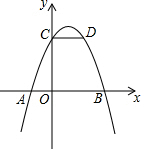 如图,在平面直角坐标系中,抛物线y=α(x-1)2+k与x轴交于A.B两点,与y轴交于C点.CD∥x轴与抛物线交于D点且A(-1,0)则OB+CD=( )
如图,在平面直角坐标系中,抛物线y=α(x-1)2+k与x轴交于A.B两点,与y轴交于C点.CD∥x轴与抛物线交于D点且A(-1,0)则OB+CD=( )