题目内容
17.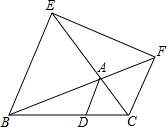 如图,从△ABC各顶点作平行线AD∥EB∥FC,各与其对边或其延长线相交于D,E,F.求证:S△DEF=2S△ABC.
如图,从△ABC各顶点作平行线AD∥EB∥FC,各与其对边或其延长线相交于D,E,F.求证:S△DEF=2S△ABC.
分析 根据平行线间的距离处处相等得到:△ADE和△ABD在底边AD上的高相等,△ADF和△ADC在底边AD上的高相等,△BEF和△BEC在底边BE上的高相等,所以由三角形的面积公式和图形间的面积的数量关系进行证明即可.
解答  证明:∵AD∥BE,AD∥FC,FC∥BE,
证明:∵AD∥BE,AD∥FC,FC∥BE,
∴△ADE和△ABD在底边AD上的高相等,△ADF和△ADC在底边AD上的高相等,△BEF和△BEC在底边BE上的高相等,
∴S△ADF=S△ADC,S△BEF=S△BEC,S△AEF=S△BEF-S△ABE=S△BEC-S△ABE=S△ABC
∴S△DEF=S△ADE+S△ADF+S△AEF=S△ABD+S△ADC+S△ABC=2S△ABC.
即S△DEF=2S△ABC.
点评 本题考查了平行线间的距离和三角形的面积.两平行线之间的距离的定义,即两直线平行,则夹在两条平行线间的垂线段的长叫两平行线间的距离.

练习册系列答案
相关题目
9. 如图,∠C=90°,DE垂直平分AB,DC=DE,则∠ADC的度数为( )
如图,∠C=90°,DE垂直平分AB,DC=DE,则∠ADC的度数为( )
 如图,∠C=90°,DE垂直平分AB,DC=DE,则∠ADC的度数为( )
如图,∠C=90°,DE垂直平分AB,DC=DE,则∠ADC的度数为( )| A. | 40° | B. | 50° | C. | 60° | D. | 70° |
6.已知反比例函数y=-$\frac{2}{x}$,下列结论不正确的是( )
| A. | 图象必经过点(-1,2) | B. | y随x的增大而增大 | ||
| C. | 图象在第二、四象限内 | D. | 若x>1,则0>y>-2 |
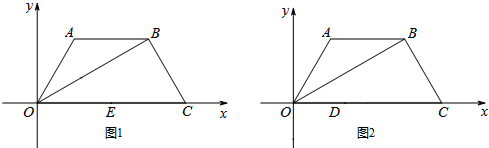
 如图,直线y=kx+4与函数y=$\frac{m}{x}$(x>0,m>0)的图象交于A、B两点,且与x、y轴分别交于C、D两点.
如图,直线y=kx+4与函数y=$\frac{m}{x}$(x>0,m>0)的图象交于A、B两点,且与x、y轴分别交于C、D两点.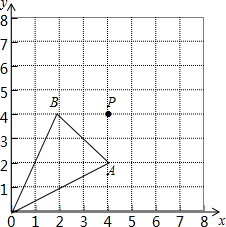 如图,在直角坐标系中,△ABO三个顶点及点P的坐标分别是O(0,0),A(4,2),B(2,4),P(4,4),以点P为位似中心,画△DEF与△ABO位似,且相似比为1:2,请在网格中画出符合条件的△DEF.
如图,在直角坐标系中,△ABO三个顶点及点P的坐标分别是O(0,0),A(4,2),B(2,4),P(4,4),以点P为位似中心,画△DEF与△ABO位似,且相似比为1:2,请在网格中画出符合条件的△DEF.