题目内容
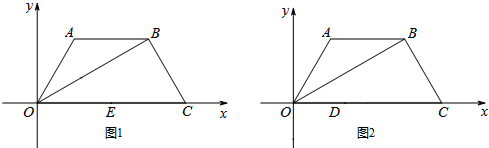
7.如图1,等腰梯形OABC的底边OC在x轴上,AB∥OC,O为坐标原点,OA=AB=BC,∠AOC=60°,连接OB,点P为线段OB上一个动点,点E为边OC中点.(1)连接PA、PE,求证:PA=PE;
(2)连接PC,若PC+PE=2$\sqrt{3}$,试求AB的最大值;
(3)在(2)在条件下,当AB取最大值时,如图2,点M坐标为(0,-1),点D为线段OC上一个动点,当D点从O点向C点移动时,直线MD与梯形另一边交点为N,设D点横坐标为m,当△MNC为钝角三角形时,求m的范围.
分析 (1)连接AE,先证明∠ABO=∠BOC,再证明△OAE为等边三角形即可得证;
(2)由PC+PE=2$\sqrt{3}$,可知PC+PA=2$\sqrt{3}$.根据三角形三边关系OB=AC≤PC+PA,列不等式即可;
(3)当AB取最大值时,AB=OA=BC=2,OC=4.分三种情况讨论:①当N点在OA上时,如图2,若CN⊥MN时,此时线段OA上N点下方的点(不包括N、O)均满足△MNC为钝角三角形.
②当N点在AB上时,不能满足△MNC为钝角三角形;③当N点在BC上时,如图3,若CN⊥MN时,此时BC上N点下方的点(不包括N、C)均满足△MNC为钝角三角形.
解答 解:(1)证明:如图1,连接AE.
∵OA=AB,
∴∠AOB=∠ABO,
∵AB∥OC,
∴∠ABO=∠BOC,
∵∠AOC=60°,
∴∠AOB=∠BOC=30°,
∴∠OBC=90°,
∵E为OC的中点,
∴OC=2BC=2OA,
∴△OAE为等边三角形,
∴OB垂直平分线段AE,
∴PA=PE;
(2)∵PC+PE=2$\sqrt{3}$,
∴PC+PA=2$\sqrt{3}$.
显然有OB=AC≤PC+PA=2$\sqrt{3}$,
在Rt△BOC中,设AB=OA=BC=x,则OC=2x,OB=$\sqrt{3}$x,
∴$\sqrt{3}$x≤2$\sqrt{3}$,
∴x≤2.
即AB的最大值为2;
(3)当AB取最大值时,AB=OA=BC=2,OC=4.
分三种情况讨论:
①当N点在OA上时,如图2,若CN⊥MN时,此时线段OA上N点下方的点(不包括N、O)均满足△MNC为钝角三角形.
过N作NF⊥x轴,垂足为F,
∵A点坐标为(1,$\sqrt{3}$),
∴可设N点坐标为(a,$\sqrt{3}$a),
则DF=a-m,NF=$\sqrt{3}$a,FC=4-a.
∵△OMD∽△FND∽△FCN,
∴$\frac{OD}{OM}=\frac{DF}{NF}=\frac{NF}{FC}$
∴$\frac{m}{1}=\frac{a-m}{\sqrt{3}a}=\frac{\sqrt{3}a}{4-a}$.
解得,m=$\frac{4-\sqrt{3}}{4\sqrt{3}+1}$=$\frac{20\sqrt{3}-28}{47}$,即当0<m<$\frac{20\sqrt{3}-28}{47}$时,△MNC为钝角三角形;
②当N点在AB上时,不能满足△MNC为钝角三角形;
③当N点在BC上时,如图3,若CN⊥MN时,此时BC上N点下方的点(不包括N、C)均满足△MNC为钝角三角形.
∵OB⊥BC,CN⊥MN,
∴MN∥OB,
∴∠ODM=∠BOC=30°,
∵OM=1,
∴OD=m=$\sqrt{3}$,
∴当$\sqrt{3}$<m<4时,△MNC为钝角三角形.
综上所述,当0<m<$\frac{20\sqrt{3}-28}{47}$或$\sqrt{3}$<m<4时,△MNC为钝角三角形.
点评 本题主要考查了等腰梯形的性质、等边三角形的判定与性质、相似三角形的判定与性质、三角形三边关系的应用以及数形结合和分类讨论等数学方法的综合运用,具有较强的综合性,旨在培养学生综合分析能力和逻辑推理能力.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 如图,?ABCD中,AE⊥BC于E,AF⊥CD于F.若AE=2,AF=3,?ABCD的周长为25,则?ABCD的面积为15.
如图,?ABCD中,AE⊥BC于E,AF⊥CD于F.若AE=2,AF=3,?ABCD的周长为25,则?ABCD的面积为15.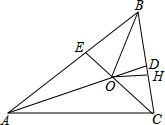 已知:如图,在△ABC中,∠BAC、∠BCA的角平分线AD、CE相交于点O.OH⊥BC于点H,连接OB.
已知:如图,在△ABC中,∠BAC、∠BCA的角平分线AD、CE相交于点O.OH⊥BC于点H,连接OB.
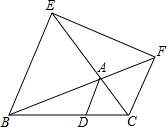 如图,从△ABC各顶点作平行线AD∥EB∥FC,各与其对边或其延长线相交于D,E,F.求证:S△DEF=2S△ABC.
如图,从△ABC各顶点作平行线AD∥EB∥FC,各与其对边或其延长线相交于D,E,F.求证:S△DEF=2S△ABC.