题目内容
12.已知函数y=(|a|-3)x2+2(a-3)x是关于x的正比例函数.(1)求正比例函数的解析式;
(2)画出它的图象;
(3)若它的图象有两点(x1,y1),(x2,y2),且x1<x2,试比较y1和y2的大小.
分析 (1)由正比例函数的定义可得到a所满足的方程,可求得a的值,可求得函数解析式;
(2)可取两点,利用描点法画出其图象;
(3)利用正比例函数的增减性可比较大小.
解答 解:(1)∵y=(|a|-3)x2+2(a-3)x是关于x的正比例函数,
∴|a|-3=0且a-3≠0,解得a=-3,
∴y=-12x;
(2)当x=1时,y=-12,且函数图象过原点,
其图象如图所示:
(3)在y=-12x中,k=-12<0,
∴y随x的增大而减小,
∴当x1<x2时,y1>y2.
点评 本题主要考查正比例函数的定义、图象及性质,掌握正比例函数的解析式为y=kx(k≠0)是解题的关键.

练习册系列答案
相关题目
3.某工厂生产一批螺帽,根据产品质量要求,螺帽的内径可以有0.02毫米误差,抽查5只螺帽,超过规定内径的毫米数记为正数,不足规定内径的毫米数记为负数,检查结果如下表.
(1)指出哪些产品是合乎要求的(即在误差范围内的)
(2)指出合乎要求的产品中哪个质量好一些,并用绝对值的知识进行说明.
| +0.030 | -0.018 | +0.026 | -0.025 | +0.015 |
(2)指出合乎要求的产品中哪个质量好一些,并用绝对值的知识进行说明.
1.点P(-1,3)关于x轴对称的点的坐标是( )
| A. | (-1,-3) | B. | (1,-3) | C. | (1,3) | D. | (-3,1) |
2.下列代数式中,符合书写规范的是( )
| A. | m÷n | B. | 2$\frac{2}{5}x$ | C. | xy | D. | a×20% |
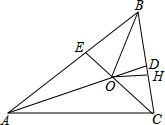 已知:如图,在△ABC中,∠BAC、∠BCA的角平分线AD、CE相交于点O.OH⊥BC于点H,连接OB.
已知:如图,在△ABC中,∠BAC、∠BCA的角平分线AD、CE相交于点O.OH⊥BC于点H,连接OB.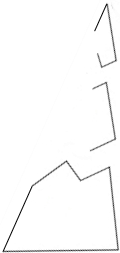 课外活动时,小明不小心将教室花架上的一块三角形玻璃打碎了,他看着地上的碎玻璃(如图)着急地说:“是我不小心打碎的.我想赶快去配一块,可玻璃已碎了,尺寸大小都不知道怎么办呢?”同学小灵说:“别急,只要你拿一块玻璃就可以去配上与原来完全相同的玻璃.”请想一想,应该拿哪一块呢?为什么?
课外活动时,小明不小心将教室花架上的一块三角形玻璃打碎了,他看着地上的碎玻璃(如图)着急地说:“是我不小心打碎的.我想赶快去配一块,可玻璃已碎了,尺寸大小都不知道怎么办呢?”同学小灵说:“别急,只要你拿一块玻璃就可以去配上与原来完全相同的玻璃.”请想一想,应该拿哪一块呢?为什么?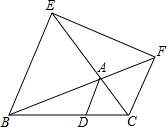 如图,从△ABC各顶点作平行线AD∥EB∥FC,各与其对边或其延长线相交于D,E,F.求证:S△DEF=2S△ABC.
如图,从△ABC各顶点作平行线AD∥EB∥FC,各与其对边或其延长线相交于D,E,F.求证:S△DEF=2S△ABC. 如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G,请判断四边形GECF的形状,并证明你的结论.
如图,在△ABC中,∠ACB=90°,CD是AB边上的高,∠BAC的平分线AE交CD于F,EG⊥AB于G,请判断四边形GECF的形状,并证明你的结论.