题目内容
20.计算:(3+2$\sqrt{2}$)2002•(3-2$\sqrt{2}$)2003.分析 先利用积的乘方得到原式=[(3+2$\sqrt{2}$)•(3-2$\sqrt{2}$)]2002•(3-2$\sqrt{2}$),然后根据平方差公式计算.
解答 解:原式=[(3+2$\sqrt{2}$)•(3-2$\sqrt{2}$)]2002•(3-2$\sqrt{2}$)
=(9-8)]2002•(3-2$\sqrt{2}$)
=3-2$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
10.已知x=1是方程x2+x-2a=0的一个根,则方程的另一个根是( )
| A. | 1 | B. | 2 | C. | -2 | D. | -1 |
8.如图,是2015年杭州市某月24日08时至25日07时的空气质量指数统计图(空气质量指数AQI的值在不同的区间,就代表了不同的空气质量水平.比如0-50之间,代表“良好”,对应的颜色为绿色;51-100之间,代表“中等”,对应的颜色为黄色;101-150之间,代表“对敏感人群不健康”,对应的颜色为橙色等等.),则根据统计图得出的下列判断,正确的是( )
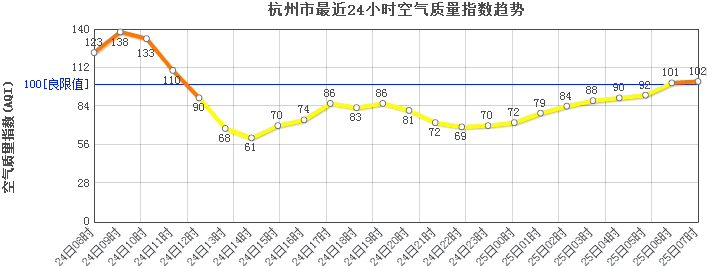

| A. | 在这个24小时中,AQI的值超过良限值时段是24日08时至24日12时 | |
| B. | 在这个24小时中,AQI对应的颜色为黄色的时段持续了20小时以上 | |
| C. | 在这个24小时中,AQI的最大值和最小值的差为77 | |
| D. | 建议中老年朋友在25日06时至07时进行晨练 |
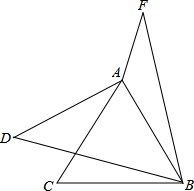 如图,已知等边△ABC,点D在AC的外侧,将BD绕点B顺时针旋转60°至BF,点F与点D相对应,连接AF,AD,AD=2,∠CBD=15°,∠AFB=30°,则AF的长为$\sqrt{6}-\sqrt{2}$.
如图,已知等边△ABC,点D在AC的外侧,将BD绕点B顺时针旋转60°至BF,点F与点D相对应,连接AF,AD,AD=2,∠CBD=15°,∠AFB=30°,则AF的长为$\sqrt{6}-\sqrt{2}$.