题目内容
 如图,已知AB是⊙O的直径,点C、D在⊙O上,∠ABC=60°,则∠D=
如图,已知AB是⊙O的直径,点C、D在⊙O上,∠ABC=60°,则∠D=考点:圆周角定理
专题:
分析:连接AC,由圆周角定理可知,∠D=∠A,由于AB为直径,∠ACB=90°,在Rt△ABC中,利用互余关系求∠A即可.
解答: 解:连接AC,
解:连接AC,
∵AB为直径,∴∠ACB=90°,
∴∠A=90°-∠ABC=90°-60°=30°,
由圆周角定理可知,∠D=∠A=30°,
故答案为:30°.
 解:连接AC,
解:连接AC,∵AB为直径,∴∠ACB=90°,
∴∠A=90°-∠ABC=90°-60°=30°,
由圆周角定理可知,∠D=∠A=30°,
故答案为:30°.
点评:本题考查了圆周角定理,直角三角形的判定与性质.关键是利用圆的直径判断直角三角形,利用互余关系求∠A,利用圆周角定理求∠D.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
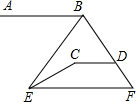 如图,AB∥CD∥EF,∠ABE=50°,∠ECD=160°,则∠BEC的度数为( )
如图,AB∥CD∥EF,∠ABE=50°,∠ECD=160°,则∠BEC的度数为( )| A、20° | B、25° |
| C、30° | D、35° |
 如图,P在∠AOB内,点M、N分别是点P关于AO、BO的对称点,如果△PEF的周长为15,则MN的长为( )
如图,P在∠AOB内,点M、N分别是点P关于AO、BO的对称点,如果△PEF的周长为15,则MN的长为( )| A、15 | B、16 | C、17 | D、18 |
该列数据0,0,1,1,1,2,3的众数是( )
| A、2 | B、0 | C、1 | D、3 |
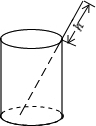 如图,一根长18cm的筷子置于底面半径为5cm.高为12cm圆柱形水杯中,露在水杯外面的长度hcm,则h的取值范围是
如图,一根长18cm的筷子置于底面半径为5cm.高为12cm圆柱形水杯中,露在水杯外面的长度hcm,则h的取值范围是 如图,点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,若∠AOC=25°,则∠BOE=
如图,点O是直线AD上一点,射线OC、OE分别是∠AOB、∠BOD的平分线,若∠AOC=25°,则∠BOE=