题目内容
11.从⊙O外一点A引⊙O的切线AB,切点为B,连接AO并延长交⊙O于点C,点D.连接BC.(1)如图1,若∠A=26°,求∠C的度数;
(2)如图2,若AE平分∠BAC,交BC于点E.求∠AEB的度数.

分析 (1)连接OB,根据切线性质求出∠ABO=90°,根据三角形内角和定理求出∠AOB,求出∠C=∠OBC,根据三角形外角性质求出即可;
(2)根据三角形内角和定理求出2∠C+2∠CAE=90°,求出∠C+∠CAE=45°,根据三角形外角性质求出即可.
解答 解:(1)连接OB,如图1,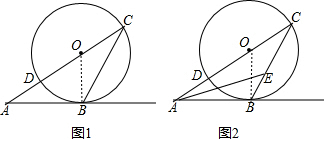
∵AB切⊙O于B,
∴∠ABO=90°,
∵∠A=26°,
∴∠AOB=90°-26°=64°,
∵OC=OB,
∴∠C=∠CBO,
∵∠AOB=∠C+∠CBO,
∴∠C=$\frac{1}{2}∠AOB$=32°;
(2)连接OB,如图2,
∵AE平分∠BAC,
∴∠CAE=$\frac{1}{2}$∠CAB,
∵由(1)知:∠OBA=90°,∠C=∠CBO,
又∵∠C+∠CAB+∠CBA=180°,
∴2∠C+2∠CAE=90°,
∴∠CAE+∠C=45°,
∴∠AEB=∠CAE+∠C=45°.
点评 本题考查了切线的性质,三角形内角和定理和三角形外角性质等知识点,能根据切线的性质得出∠ABO=90°是解此题的关键.

练习册系列答案
相关题目
 如图,点C是以AB为直径的⊙O上一点,CD是⊙O切线,D在AB的延长线上,作AE⊥CD于E.
如图,点C是以AB为直径的⊙O上一点,CD是⊙O切线,D在AB的延长线上,作AE⊥CD于E.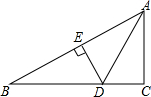 如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=3,则DE的长为1.
如图,在Rt△ABC中,∠C=90°,∠CAB的平分线交BC于D,DE是AB的垂直平分线,垂足为E,若BC=3,则DE的长为1.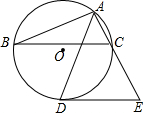 如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,过点D作DE∥BC交AC的延长线于点E.
如图,△ABC内接于⊙O,AD平分∠BAC交⊙O于点D,过点D作DE∥BC交AC的延长线于点E.
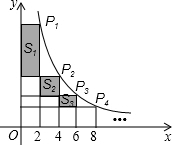 如图,在反比例函数y=$\frac{10}{x}$(x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为2,4,6,8,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn=10-$\frac{10}{n+1}$(用含n的代数式表示)
如图,在反比例函数y=$\frac{10}{x}$(x>0)的图象上,有点P1,P2,P3,P4,…,它们的横坐标依次为2,4,6,8,…分别过这些点作x轴与y轴的垂线,图中所构成的阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1+S2+S3+…+Sn=10-$\frac{10}{n+1}$(用含n的代数式表示)