题目内容
20. 如图,在等边三角形ABC的AC、CB边的延长线上各取一点P、Q,使得AP=CQ,直线AQ,BP相交于点O,则∠BOQ=120°.
如图,在等边三角形ABC的AC、CB边的延长线上各取一点P、Q,使得AP=CQ,直线AQ,BP相交于点O,则∠BOQ=120°.
分析 由△ABC为等边三角形,利用等边三角形的性质得到AB=BC,∠ACB=∠ABC=60°,利用等角的补角相等得到夹角相等,利用SAS得到三角形ABQ与三角形BCP全等,利用全等三角形的对应角相等得到∠AQB=∠BPC,利用外角性质及等量代换即可得证.
解答 证明:∵△ABC为等边三角形,
∴AB=BC=AC,∠ACB=∠ABC=60°,
∴∠ABQ=∠BCP=120°,
∵AP=CQ,
∴AP-BC=CQ-BC.
即BQ=CP,
在△ABQ和△BCP中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABQ=∠BCP}\\{BQ=CP}\end{array}\right.$,
∴△ABQ≌△BCP(SAS),
∴∠AQB=∠BPC,
则∠AOB=∠OQB+∠OBQ=∠CPB+∠CBP=∠ACB=60°,
∴∠BOQ=180°-∠AOB=180°-60°=120°.
故答案为:120°.
点评 此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
相关题目
9.已知:$\frac{x+y}{x-2y}=\frac{5}{2}$,则$\frac{x}{y}$的值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | 3 | D. | 4 |
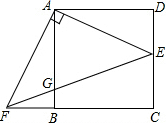 已知,在正方形ABCD中,AB=2,点E是CD边上的一个动点,点F在CB的延长线上,∠EAF=90°.
已知,在正方形ABCD中,AB=2,点E是CD边上的一个动点,点F在CB的延长线上,∠EAF=90°. 尺规作图:
尺规作图: